小１算数「いくつといくつ」指導アイデア《半具体物の操作による５の構成》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2023.07.19

単元の展開

第１時　「たりるかな」一対一対応による、集合の要素の個数の多少や相当の比較
▼
第２時　「おなじかずのなかまをさがそう」１～５個のものの数を数えることと、数字の書き方
▼
第３時　１～５の数について、具体物、半具体物、数図、数字、数詞を相互に関連付けること
▼
第４時（本時）「５はいくつといくつ」半具体物の操作による５の構成
▼
第５時　「おなじかずのなかまをさがそう」６～10個のものの数を数えることと、数字の書き方
▼
第６時　６～10の数について、具体物、半具体物、数図、数字、数詞を相互に関連付けること
▼
第７時　「６はいくつといくつ」半具体物の操作による６の構成
▼
第８時　「７はいくつといくつ」半具体物の操作による７の構成
▼
第９時　「８はいくつといくつ」半具体物の操作による８の構成
▼
第10時　「９はいくつといくつ」半具体物の操作による９の構成
▼
第11時　「10はいくつといくつ」半具体物の操作による10の構成
▼
第12時　10の構成の理解、数の構造的な見方を活用して、ものの数を数えること
▼
第13時　１～10の数の大小や系列
▼
第14時　１つもないことを０と表すこと

本時のねらい

「５」についての数当てクイズの問題づくりについて、ビー玉をおはじきに置き換えて考えたり、片方が１つ増えると、もう片方の数が１つ減るという規則性に気付いたりすることにより、５の構成を理解することができる。

評価規準

５の数の合成・分解ができる。（知識・技能）
一方が１増えれば他方は１減るという規則性に着目することにより、５の合成・分解を順序立てて考えることができる。（思考・判断・表現）
数当てクイズを通して、「５」の合成・分解に関心をもち、いくつといくつという見方で数を表そうとしている。（主体的に学習に取り組む態度）

本時の展開

「５」のかずあてくいずをしよう！

今日は、先生やクラスのお友達と「５」の数当てクイズをしますよ。

楽しそう。早くやってみたい。

先生は今、ビー玉を持っています。何個あるか、みんなで数えましょう！

１、２、３、４、５。ビー玉は全部で５個あります。

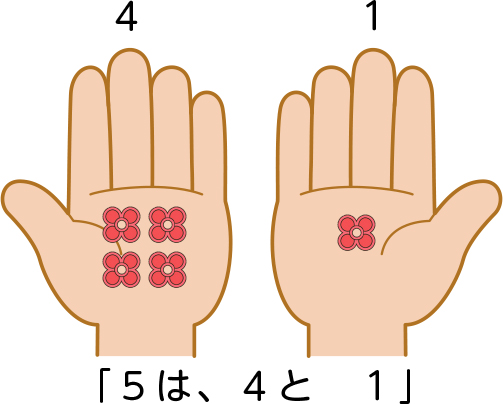
ビー玉は５個ありますね。さて、ここで「５」の数当てクイズを出しますよ。５個のビー玉を左手と右手に分けます。今、左手の中にビー玉が４個あります。右手の中には、ビー玉はいくつあるでしょう。

分かった。１個です。

答えは本当に１個で合っていますか。

１個でいいと思うけど、自信がないな……。

左手の中は、本当に１個でいいのか、心配な人もいますね。１個かどうか、確かめることはできますか。

「本当に？」と問いかけることで、『ビー玉をおはじきに置き換えて考える』というアイデアを子供から引き出しましょう。

先生みたいにビー玉を持っていないから、確かめられません……。

分かった。ビー玉の代わりに、私たちの持っているおはじきを使えばいいよ。

それでは、自分が持っているおはじきで確かめましょう。右手と左手の絵が書いてあるプリントを配るので、それをノートに貼ります。貼ったら、その上におはじきを置いて確かめましょう。

※重要！！
手のイラストが描かれたワークシート（下段参照）を学級全員に配付し、ノートに貼らせます。その後、イラストの上におはじきを置かせましょう。単元を通して、同じイラストを活用するので、この段階で使い方を学級全員に理解してもらいましょう。
また、黒板にも、このイラストを拡大したものを掲示し、子供の手元に置けるおはじきの操作を再現します。

おはじきを置くとよく分かるね。左手に４個で、右手に１個。数えると全部で５個になる。

右手の中には、１個のおはじきがあるはずね。

正解です。右手の中にはおはじきが１個ありました。左手が４個のとき、右手は１個でした。このことを、『５は４と１』と言います。今日は、このような言い方をするので、みんなで覚えましょう。