小6算数「6年のまとめ①(変化と関係)」指導アイデア《速さの概念を用いて走行速度を比較しよう》
執筆/埼玉県公立小学校教諭・村井幸太
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
本時 17/25(変化と関係3/6)
ねらい
速さは単位量当たりに進む道のりであることを振り返り、その考えを用いて実際に競走できないものでも速さ比べができるよさを知る。
評価規準
速さが単位時間当たりに進む道のりであることを理解し、それを踏まえて速さを比べたり速さについて説明したりすることができる。
問題場面
こうたさんは100m走の世界記録がウサイン・ボルト選手の9.58 秒であることを調べました。ここからこうたさんは「人類最速の選手と犬、どちらが速いのだろう」という疑問を持ちました。そして、飼っている3匹の犬に100mを走らせようとしました。
しかし、どの犬もなかなか100mをまっすぐ走りません。とりあえずまっすぐ走った道のりとそのタイムを記録しました。
3匹の犬とボルト選手では、どれが一番速く走れるのか考えましょう。
みなさんは犬たちが人類最速の選手に勝てると思いますか。
どの犬も勝てると思います。
ボルゾイは見た目から速そうです。
チワワは負けそう。
でも、人間の方が速いんじゃないかな。
印象だけで決めてしまうのはだめですね。実際の結果がこれです。(表1提示)
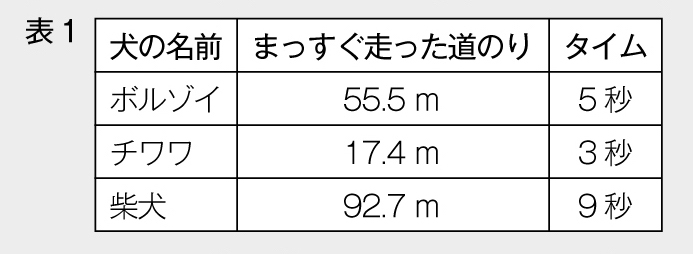
あれ? 3匹の犬はどれも100m走ってない!
どの犬も100mをまっすぐ走れなかったので、まっすぐ走った道のりとそのタイムを調べました。
確かに犬には100mまっすぐ走るのはむずかしいよね。
やっぱりこれでは人と犬の競走は無理ですかね……。この条件を使って、ボルト選手に勝てるかどうか考えることはできませんか。
速さで学習したことを使って、犬も100m走ったとしてタイムを求めればできます。
秒速の考えを使うと、速さで比べられるよ。
なるほど、「速さ」ですか。では、速さを使って比べてみましょう。また、どれが一番速いのか、その理由や、速さを利用することでどんなことが分かるのか、説明できるようにしましょう。
本時の学習のねらい
速さの意味を振り返り、速さ比べから分かることを説明しましょう。
見通し
速さってどういうことだろう。速さを比べるためには、どうしたらいいだろうか。
道のりか時間のどちらかをそろえれば比べられるよ。
速さは、単位時間にどれだけ進んだかを表したものだよね。速さは「道のり÷時間」で求められたから、それを使って求めよう。
速さが分かれば、犬たちが100mを走ったら、どれくらいのタイムになるかも求められるね。
自力解決の様子
A つまずいている子
それぞれの犬の速さについて公式を使って求めたが、犬とボルト選手とどちらが速いか説明できない。
B 一つの階級に着目して考えている子
速さが単位時間当たりに進む道のりであることを理解し、それぞれの犬の秒速を求め、そこから9.58秒で走った道のりや100mを走った時間のどちらか片方を求めて、比べている。
C ねらい通り解いている子
B児の考え方を、道のりや走った時間の両方を求めたり、ボルト選手の速さを求めたりするなど、様々な方法で比べている。また、数直線や式を利用することで比例関係を明らかにし、説明している。
学び合いの計画
A児のように、速さについて公式のみを覚えているだけで、特に意味を理解していない児童がいることが考えられます。そこで、速さは時間と道のりという2つの数量を組み合わせてつくった数量であることや、単位時間当たりに進む道のりであるということをしっかりと押さえ、説明できるようにすることが大切です。
イラスト/オモチャ
『教育技術 小五小六』2022年2/3月号より