５年生「比例」「割合」など【「算数つまずき防止」ここがポイント！#６】

算数は一つつまずくと、その後の学習が進みにくくなる教科ですが、どのような授業づくりをすれば、つまずきを防止できるのでしょうか。今回は５年生「比例」「割合」などの内容を、青森県西目屋村立西目屋小学校・浅田鶴予教諭に伺いました。

青森県西目屋村立西目屋小学校・浅田鶴予教諭

　　　監修／弘前大学教授・中野博之

５年生の学習の約半数は「割合」など、「比例」に関わる単元

５年生の算数の学習で多くの子供たちがつまずくのは、「割合」だと言われます。私の学校で使用している５年生の教科書では年間20程度の単元がありますが、そのうち「割合」に関係のある単元は10程度もあります。「割合」も、結局は「比例」の考え方が基になっていますから、「比例」に関係のある単元が、５年生では半分もあるということです。ちなみに本校の教科書では、まず「比例」の単元があり、次に「平均」がありますが、一定量あたりでならしていくという点では「比例」につながっていきます。また、「速さ」は「比例」に関係しますが、「速さ」も一定の時間あたりに移動する距離をならしたものですから、「平均」にも関わるわけです。そのほかにも、「単位量あたり」や「割合」と続きますが、このように「比例」に関わっていく単元はたくさんあるのです。

ちなみに、加法や減法に関する学習は大半が３年生あたりで収束していきますので、高学年の「数と計算」の領域では、「比例」に関係する学習が大半になり、つまずきの原因はそこにあります。そのため、５年生の「比例」や「割合」でつまずく子供の多くは、３年生、４年生の「比例」（「比例」という言葉は学習しませんが）に関係する学習内容（＝乗法や除法）から尾を引いている場合が多く見られるのです。

では、「割合」の何がむずかしいかというと、大小関係を比較するときも低学年の加法や減法の場合は端を０にそろえて長ければ大きいし、短ければ小さいと判断していたものが、「割合」になると数の異なるものを同じ幅に合わせて、その中でどれだけを占めるかを比べていくことになり、そのことがむずかしいと考えられます。そのようなむずかしさがある単元なのですが、若い先生方の指導では、自分自身が受験戦争を勝ち抜く過程で学習した計算の仕方や処理の手続きなどを子供に教え込み、繰り返し反復練習をさせるといった例を見ます。しかし、そういった指導方法は対症療法にはなっても、本質的な意味理解にはつながらないと思うのです。

では、どう考えればよいかということですが、新しい単元に入るときに教師が、「内容を落とさずやらせよう」とか「とりあえず計算できるようにしよう」と考えるのではなく、「新しい単元も、比例に関わる見方・考え方だからふり返りながら学習しよう」というように、見方・考え方を意識して指導することが必要だと思います。中野博之教授は、よく「数学的な見方・考え方は、習慣のようなものだから一朝一夕に身に付くものではない」と言われます。習慣は一度身に付くと忘れないのですが、新しい習慣を身に付けるには時間もかかります。ですから、そのときにできないから「この方法でとりあえず計算できるようにしよう」とか、「反復練習を徹底しよう」などと、短期的な目標をもつだけではなく、「ここでは十分には理解できていない子供もいるけれど、この考え方が出てくる次の内容や、その次の内容ではどうアプローチしようか」というように長期的な展望をもって指導することが大切だと思います。

特に５年生の学習内容は、先に説明した通り全単元の半数ほどで比例の関係が使われているわけですから、乗法や除法が出てきたときには、「あっ、これ比例だ」「わり算だ」「単位量あたりだ」と教師が意識し、子供たちにも気付かせていくことで、子供たちの理解もずいぶんと変わってくると思います。

比例に関わる単元では、ニ重数直線を使って指導

さて、では「比例」や「割合」の具体的な指導方法について紹介をしていきましょう。

「比例」や「割合」を子供たちが学習するうえで効果的な方法は、数直線だと私は考えています。２数直線とか二重数直線と呼ばれるものです。ほかにも、面積図などを使う方法もありますが、面積図は分数÷分数になると使うことがむずかしくなります。そこで私は、４年生以降の「比例」に関わる学習では、すべて数直線を使っています。

数直線は左から始まって右にいくほど数が増えていきますよね。子供たちはこの数直線を右側にいくのはかけ算で、左にいくのがわり算だととらえがちです。それは、子供たちがかけ算を最初に学習した２年生のときに累加で学んでいるからです。２＋２＋２が２×３だから、かけ算をすると答えは大きくなる（＝数直線上を右にいく）と思っているわけです。わり算は逆に、累加の１個分を求めるから当然、小さくなる（＝数直線上を左にいく）と思っているのです。

ところが、現行学習指導要領では４年生で小数倍が導入されました。これによって、「なんで、かけ算なのに左にいくの？（小さくなるの？）」という大革命が起きます。かけ算が「累加」から「割合」へと意味が拡張されるわけです。ですから、４年生で初めて数直線を学んだときに、「右にいくとかけ算、左がわり算」と覚え込んでいると、困る子供が出てくるわけです。

そのため、私が以前、４年生を担任したときには、例えば「１dLで２㎡塗ることのできるペンキがあります。２dLでは何㎡塗ることができますか？」というような、式だけで解いてもすぐに答えが出るような問題があったとしても、必ず数直線を描かせるようにしました。そして子供たちには、「（単位量の）１から出るときは、右にいく場合も、左にいく場合もかけ算だよ」と指導したのです。

こうした問題を見ると教師は、「かけ算で解決する問題があると、すべて比例が前提だ」と思っているのですが、子供たちはそうは思っていなかったりします。この、ペンキの問題でも、「２dLになると、塗れる面積は増える？　減る？」と問うと、「増える」と答えます。「じゃあ、どのくらい増える？」と問うと、多くは「２倍に増える」と答えます。しかし、私が担任する子供たちのなかには、「でもね、先生、実際にはピッタリ２倍は塗れなかったりするよ」と言う子供もいるのです。現実にはその通りであり、あくまで算数の世界で比例の関係があるから「ペンキが２倍になると、塗れる面積も２倍になる」ということを意識させることが大切だと思います。

ちなみに、「比例」という言葉は出てきませんが，簡単な比例の例は４年生で学習しますから、そのときから二重数直線の片方の数直線上を動くと、もう片方も一緒に動いていくイメージをさせていくことが理想的です。しかし、４年生のときにそうした学習をしていない子供もいますから、それを確認するために、子供たちに「片方が２倍になると？」と聞いてみるのです。そうすると、「もう片方は２倍」と答えます。そこで、「『もう片方は』なの？」と問い返すと、「ああ違う。『もう片方も』だ！」と答えます。そのような細かいことから、比例は伴って変わる量であることを意識させていくことが大事なのです。

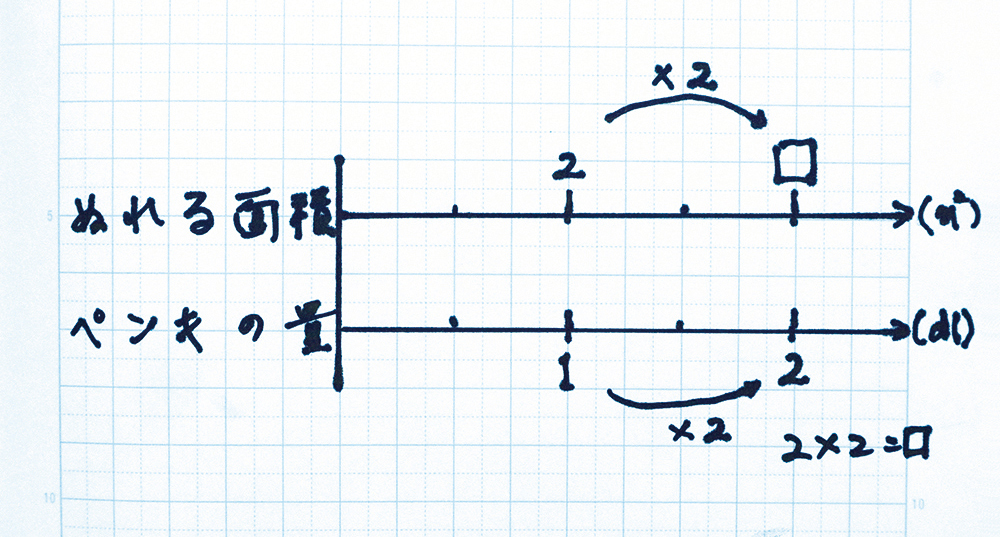
話を戻しますが、先のペンキの問題を学習するときにも二重数直線を使います（資料１参照）。この図を使えば、求める面積は、２×２だという演算決定もできますし、もし数が少々大きくなっても大体の答えがイメージできるのです。これを計算すると、すぐに４が出てくるわけですが、そのときも答えが出たら終わりにはしないことが大事です。「４㎡と出たら、そこから本当に最初の１dLは２㎡に戻るかどうかやってごらん」と声をかけて、自分の出した答えが正しいかどうか確かめさせるとか、この□が２㎡よりも大きくていいのか確認してみるとか、そうしたことを積み重ねさせていくことが大事です。そうした積み重ねをすることで、「比例」に関わる学習でおかしな答えが出たときにも、「これ、計算間違えたかな？」と気付く子供に育っていくのです。

こうして、二重数直線の使い方を身に付けると、何畳の部屋に子供が何人いるとか、何秒で何m走るとか、何個で何㎏の重さとか、単位が変わってもこれを使って問題を考えることができます。さらに二重数直線は、わり算で求める問題の場合にも使えます。先ほどのペンキの問題であれば、数直線は同じです。２㎏で４㎡塗れることが分かっていて、１dLあたりの塗れる面積を□にして求める問題であれば、１以外から出て考えるわけですから、わり算で求めるのですが、二つの数直線を描いて比例関係を見ていくこと自体は変わりません。

このようにして、５年生の「比例」に関わる単元を繰り返し学習しているうちに、子供たちは「先生、前も出てきたよ」とか、「前に勉強してきたことと同じだね」と言うようになっていきます。そうした学習のなかで、わり算とかけ算も統合されていくわけです。そのような「見方・考え方」を働かせ、本質的な理解に導くのではなく、「３皿では」とか、「分けると」といった問題文の言葉に着目した演算決定の指導ばかりしていると、「これは、わり算の問題かな」「いや、かけ算の問題だよ」と、わり算かかけ算かという結果だけにこだわる子供に育ちます。しかし、先のような学習を繰り返していると、わり算の問題かかけ算の問題かにこだわるのではなく、「これは～を求めるから、かけ算になる」「これは～だからわり算だ」と理由まで考えられるようになっていくのです。

学習のまとめの表現を吟味し、ふり返りを大切にする

こうして、数直線を使って「比例」に関わる問題の解決ができるようになると、当然、ほかの単元でも数直線を書いて問題解決できるようになります。例えばハムスターがいて、Aは「マット２枚にハムスターが12匹」、Ｂは「マット３枚にハムスターが15匹」いる場合、どちらが込んでいるかという問題があるとします。この場合も、二重数直線を書けばできるわけです。マット数もハムスターの数も、ＡとBとではそろっていないから比べられないので、数をそろえようということになって、１枚で何匹かなとなって、Ａは６匹、Ｂは５匹となって、Ｂのほうが込んでいるとなるわけです（資料２参照）。

このように数直線を使えるようになれば、単位が変わっても、どこが□になっても分かるようになります。それは、「比例」でも「割合」でも「速度」でも同じです。ですから、比例に関わる問題（乗除の問題）は、同じ道具を使ってずっと学習することが重要で、当然のことですが、同じ道具が使えるということは同じ原理原則があるということなのです。

また「比例」に関わる別の単元、次の学びでも使えるような学習のまとめを考えることも大事です。つまり、まとめで単なる処理の手続きをまとめるのではなく、なぜそうなるのかをまとめるということです。例えば、小数倍の学習でも、まとめで「小数点を下ろします」という表現がされているものを見たりしますが、「小数点は下ろせばいい」と覚えてしまうと、別の問題で間違いも生じます。そうではなく、「小数は10倍して計算した後で、10で割ってもとに戻します」というように、意味理解を図り、別の場面でも使えるようにすることが大切です。計算や処理の手続きを整理するのではなく、なぜそうなるのかという本質を子どもが考えられるようにまとめていくということです。理解がむずかしい内容だからこそ、安易に特効薬を求めるのではなく、本質的な体質改善（本質的な意味理解）ができるよう、繰り返し同じ見方・考え方を働かせながら学んでいくようにすることが大切なのだと思います。

さらに、子供が「見方・考え方」を働かせていくようにするためには、学習のふり返りも大事です。問題解決の方法を学習した後で、「この方法、どこかで見たな」とか、「この見方（や考え方）、どこかでやったな」とふり返ることができるようにしたいものです。そのために、「これ、前もやらなかったっけ？」とか「どこかで見たような…」と、先生が意図的につぶやくことを口癖にして、子供たちがそういう視点で見られるようにしていくとよいだろうと思います。

最後に、繰り返しになりますが、どの先生も思われる通り、「割合」など、「比例」に関わる問題は子供たちにとってむずかしい内容だと思います。むずかしい内容だからこそ特効薬はないと言わざるを得ません。しかし、５年生の間に10くらいもの単元で比例を使って学習をすることができるのですから、そのためにシンプルで共通して使える道具を使って、繰り返し学習していくことで、より確かな理解を図っていきたいものです。

６年生　「分数のわり算」【「算数つまずき防止」ここがポイント！#７】はこちらです。

取材／矢ノ浦勝之