小6算数「比例と反比例」指導アイデア《水深と時間の関係から反比例を学ぼう》
執筆/埼玉県公立小学校教諭・澁谷拓也
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
(本時11/15時)
ねらい
伴って変わる2つの数量に着目し、比例と対比して考えることで、反比例の関係を理解する。
評価規準
反比例する2つの数量の関係について、比例の関係を基に表などを用いて説明することができる。
問題場面
深さが60㎝の水槽に水をいっぱいに入れるとき、1分あたりに入る水の深さを1㎝、2㎝、3㎝…と変えていくと、それに伴って水槽がいっぱいになる時間はどのように変わりますか?
水の深さが1㎝、2㎝、3㎝と2倍3倍になるから、時間も2倍3倍になると思います。
でも、1分間で1㎝ずつ深くなるのだから、いっぱいになるまで60分かかります。2㎝ずつ深くなると30分かかるから、深さが2倍になっても時間は2倍にならないよ。比例じゃないです。
前時に学習した比例の関係とは違うのでしょうか。
1分間に入れる水の深さが増えると、時間はどんどん短くなりそうです。
確かに、入れる水の深さを2倍にしたら、時間は[MATH]\(\frac{1}{2}\)[/MATH]になりそうだね。
比例の時と同じように関係を表に表すと、変化の様子が見られると思います。
では、入る水の深さと水槽いっぱいになる時間がどのように変化するのか表に表して考えよう。
本時の学習のねらい
2つの数量の関係を表に表し、どのように変化するのか考えよう。
見通し
表を使って、水の深さを上の段、時間を下の段に書いて、水の深さが1、2、3㎝…と変わる時の時間を求めてみよう。
比例の時と同じように、表を横にみながら→を引いて深さの変化がどうなるか調べてみよう。
1分あたりに入る水の深さをx、水を入れる時間をyとして関係を表せないかな。
自力解決の様子
A つまずいている子
・表に→をかき入れることができているが、深さの変化に対し、時間が何倍かを求めることができない。
・水を入れる時間の変化を小数倍で表してしまい、2つの数量の関係を正しくとらえることができていない。
B ねらいどおりに解決している子
1㎝から2倍、3倍になる量へ、→と何倍になるのかを書き入れることで、深さと時間の関係をとらえている。
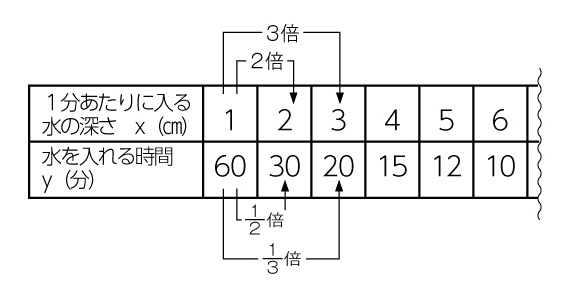
C 進んでいる子
xが1㎝を基に2、3、…倍にした の値の変化だけではなく、xが3㎝を基に2倍しても、yの値が[MATH]\(\frac{1}{2}\)[/MATH]倍になっていることを説明している。
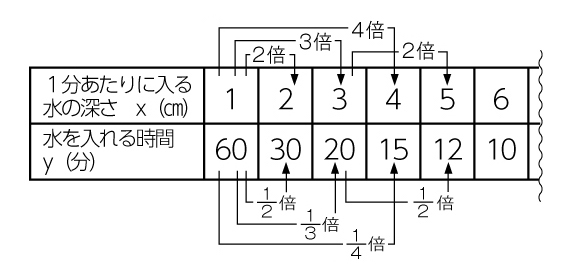
学び合いの計画
児童は、これまでの比例の学習で表を基に「変化」や「対応」について学んできました。ここでは比例の学習で学んだ2つの数量の関係を表から読み取る方法について再確認し、反比例の場面での変化の様子の違いを対比することにより、理解を深めることが大切です。
イラスト/横井智美
『教育技術 小五小六』2021年10/11月号より

