小5算数「平均・単位量当たりの大きさ」指導アイデア
執筆／新潟県公立小学校教諭・石塚正人
編集委員／文部科学省教科調査官・笠井健一、新潟県公立小学校校長・間嶋哲
目次
本時のねらいと評価規準（本時の位置 7／13時）
ねらい
広さと人数の2量の関係である「混み具合」について、一方の量を揃えればもう一方の量で比べられることを理解し、式を図や数直線と関連付けて「単位量当たりの大きさ」で比べることのよさに気付くことができる。
評価規準
「単位量当たりの大きさ」で2つの数量を比較している。
問題場面
マットの上に子どもが乗っています。A、B、Cのどのマットが一番混んでいるでしょうか？
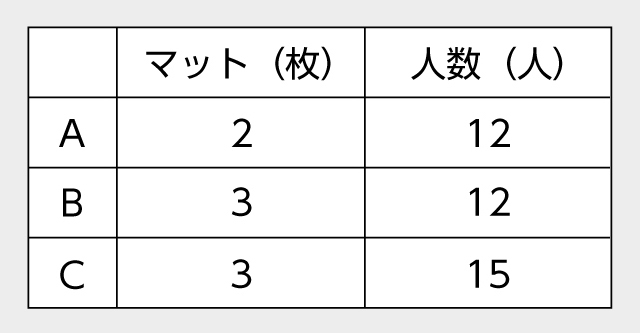
どのマットが混んでいるのか、3つの選択肢からはすぐに答えられないことを確認する。そして、広さと人数のどちらか一方の量が揃っていれば、もう一方の量で比較できることを理解させる。さらに、AとCは広さも人数も揃っていないことから、どうやって比べたらよいのかという問いをもたせる。
どのマットが混んでいるのか、3つを一度に比べることはできません。
では、すぐに比べられるのは、どれとどれですか。
AとBです。人数が同じなのだから、マットの枚数が少ないAの方が混んでいます。
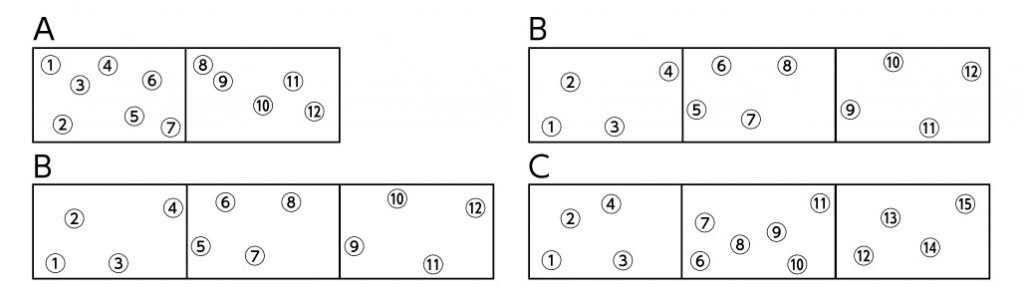
BとCも比べられます。同じマットの枚数で人数が多いCの方が混んでいます。
でも、AとCは、広さも人数も違うから比べられません。
本時の学習のねらい
広さも人数も違う2つを比べるには、どうしたらよいだろうか。
見通し
広さと人数のどちらかが同じなら比べられるよ。
マットと人の図をかいて考えてみよう。
平均の考えを使えば説明できそうだよ。
自力解決の様子
A つまずいている子
「マットと人数の2つの量しかないから、とりあえずわり算をしてみよう」
・何を求めているのか分からない子
B 素朴に解いている子
「マットと人を図で表して、人を動かしてみよう」
・図を用いて考えている子
C ねらい通り解いている子
「マット1枚に何人いるのか（1人がマットをどれくらい使えるか）で考えてみよう」
・単位量当たりの大きさで考えている子
学び合いの計画
見通しの場面において、「どちらか一方が揃っていれば、もう一方の量で比較することができる」ことを確認することが大切です。ただし、Aのように、立式して求めた値が何を表しているのか理解していない子供は少なくありません。全体発表の場面では、マットと人を図で表し、マット1枚に乗っている人の数を見えるようにしましょう。
また、マットと人数の関係を数直線に表すことで、マット１枚あたりの人数を求める式が見えることを押さえましょう。このように、式を図や数直線と関連付け、求めた値にどんな意味があるのかを確認しましょう。さらに、選択肢が増えた場合でも一度に比較でき、公倍数で揃える処理の面倒さがないといった、「1㎡当たり」や「1人あたり」など「単位量当たりの大きさ」で考えることのよさを子供に気付かせましょう。
ノート例
全体発表とそれぞれの考えの関連付け
アの考え
1枚のマットに同じ人数が乗っていることになるよう、人を動かします。
イの考え
マット1枚に平均何人いるかで比べます。
Ａ 12÷2＝6
＜マット1枚に6人＞
Ｃ 15÷3＝5
＜マット1枚に5人＞
ウの考え
1人に使っているマットで比べます。
A 2÷12＝0.166…
＜1人がマット約0.17枚＞
C 3÷15＝0.2
＜1人がマット0.2枚＞
2枚のマットを12人で分けると考えると……、
1人分のマットが分かるね。
Aはマット1枚に6人ずつ、Cはマット1枚に5人ずつ乗っていると分かるね。
私は式がよく分からないんだけれど……。
数直線をかくといいよ! まず、マット2枚に12人いるよね。
次に、マット1枚何人いるかを知りたいんだから、□をかいて……。
こうすると、比例みたいに「÷2」になるよね。だから、12÷2だよ。
そうか! 12÷2の式は、マット1枚に平均何人乗っているのかを表しているんだね。
これなら、Bもすぐ分かりそうだよ!
12÷3＝4 ＜Bはマット1枚に4人＞
学習のねらいに正対した学習のまとめ
「マット1枚あたりの人数」「1人あたりのマットの枚数」で比べればよい。
評価問題
6両に1080人乗っている電車と8両に1456人乗っている電車では、どちらが混んでいますか?
子供に期待する解答の具体例
1080÷6＝180 1456÷8＝182
だから8両の電車が混んでいる。
本時の評価規準を達成した子供の具体の姿
1両あたりの人数で比較している。
感想例
どうやって比べればよいか分かりました。マット1枚あたりで比べると、人数が多い方が混んでいるとなるので、これからこの考えを使っていきたいです。
『教育技術 小五小六』 2021年10/11月号より
