小6算数「およその面積と体積」指導アイデア《およその面積の求め方》

執筆/新潟県新潟市立総合教育センター指導主事・竹内直也
監修/文部科学省教科調査官・笠井健一、新潟県新潟市立新津第一小学校校長・間嶋哲

目次
単元の展開
第1時 身の回りのもののおよその面積について、方眼を工夫して数えて求め方を考える。
▼
第2時(本時)地図上の複雑な図形の概形を捉え、都市などのおよその面積の求め方を考える。
▼
第3時 いろいろな立体の概形を捉え、およその体積や容積の求め方を考える。
▼
第4時 学習内容の定着・習熟を図る。
本時のねらい
直線で構成されない複雑な図形の面積について、求積公式を使える基本図形として概形を捉えて、およその面積を求める方法を考えることができる。
評価規準
直線で構成されない複雑な図形の概形を基本図形として捉えて、およその面積を求め、求め方を説明することができる。
本時の展開

これは、日本でいちばん面積が大きい都市・岐阜県の高山市の形です。高山市の面積は約何㎢でしょうか。
この図だけでは、面積は分かりません。
前の時間みたいに、マス目が欲しいです。
では、方眼上の地図を見せましょう。これです。
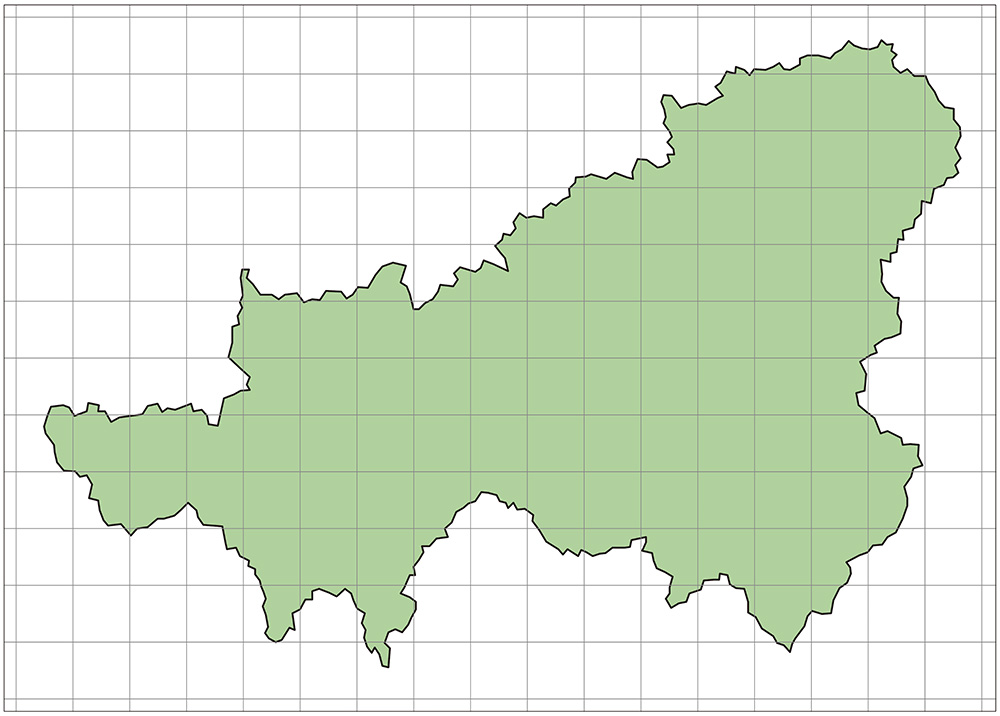
マス目の一辺の長さが5㎞ってことは、1マスで25㎢だね。
でも、マス目がいっぱいだなあ。
しかも、ぐにゃぐにゃしているから、マス目を一つずつ数えるのは大変そう……。

ぐにゃぐにゃした形のおよその面積は、どうすれば求められるだろうか。
見通し
もっと、きちんとした形だったら簡単なのに。長方形とか。
およその面積だから、だいたいでいいってことだよね。
正確ではないけれど、大ざっぱに見れば三角形っぽいよ。
○○さんの言った、「三角形っぽい」形が見えますか。
見えます! 確かに三角形っぽい。こんなふうに考えれば、だいたい三角形に見えるでしょ。
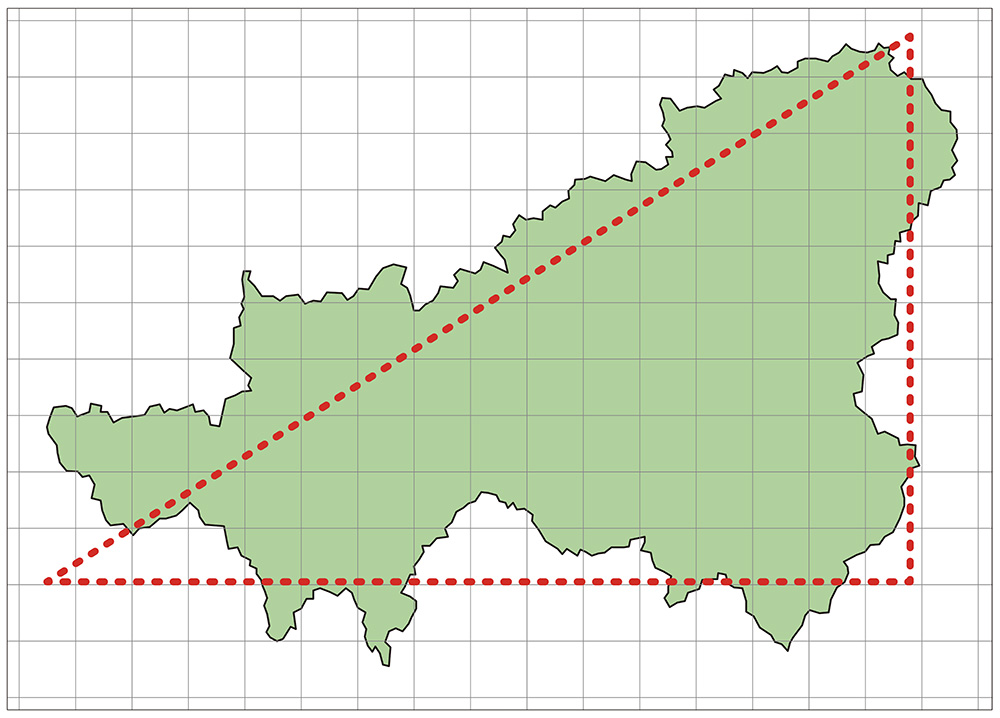
本当だ。あ! 僕は、台形が見えたよ。
だいたい三角形、だいたい台形と見れば、公式を使っておよその面積が求められるね。

本単元の学習で最も大切なことは、「概形を捉える」ことです。つまり、子供が「だいたい三角形」「だいたい台形」と言ったように、複雑な図形のおよその形を既習の基本図形と見なす見方です。しかし、初めから三角形や台形をかき込んだ状態で図形を提示してしまっては、そのような見方を子供から引き出すことはできません。そこで、「三角形っぽい」という見方を発揮した子供の発言を取り上げ、代表の子供に三角形や台形などの基本図形の辺に当たる部分を指でなぞらせたり、一辺だけ引かせたりして、概形を捉える見方を学級全体に徐々に広げていくとよいでしょう。
自力解決の様子
A つまずいている子
図形をどう見たらよいかが分からず、元の図形を数本の直線で囲んで直線図形に変形しているだけで、求積できないでいる。
B 素朴に解いている子
図形の概形を三角形や台形などの基本図形とおよそ見なしているものの、元の図形を囲むように作図して面積を求めている。
C ねらい通り解いている子
図形の概形を三角形や台形などの基本図形と見なし、過不足を考慮したちょうどよい大きさで作図して面積を求めている。
学び合いの計画
自力解決の時間は短めに設定し、多くの子供が解決のアイデアをもてた段階で、一度全体での検討に移ります。
イラスト/横井智美

