小5算数「合同な図形」指導アイデア《合同な三角形をかくための条件》
執筆/福岡教育大学附属福岡小学校教諭・石橋大輔
監修/文部科学省教科調査官・笠井健一
福岡教育大学教授・清水紀宏
単元の展開
第1時 図形を重ね合わせ、合同な図形について知る。
▼
第2時 合同な図形の対応する頂点、辺、角について調べる。
▼
第3時 図形を1本の対角線で分けてできる三角形が、合同かどうか確かめる。
▼
第4時(本時)合同な三角形をかくための条件について話し合う。
▼
第5時 合同な四角形をかくための条件について話し合う。
本時のねらい
図形を構成する要素に着目し、合同な三角形をかくための条件を理解することができる。
評価規準
合同な三角形をかくために、すべての辺の長さや角の大きさを調べる必要はないことを理解し、三角形が決まる条件を見出すことができる。(思考・判断・表現)

三角形ABCと合同な三角形をかくには、どうすればよいですか。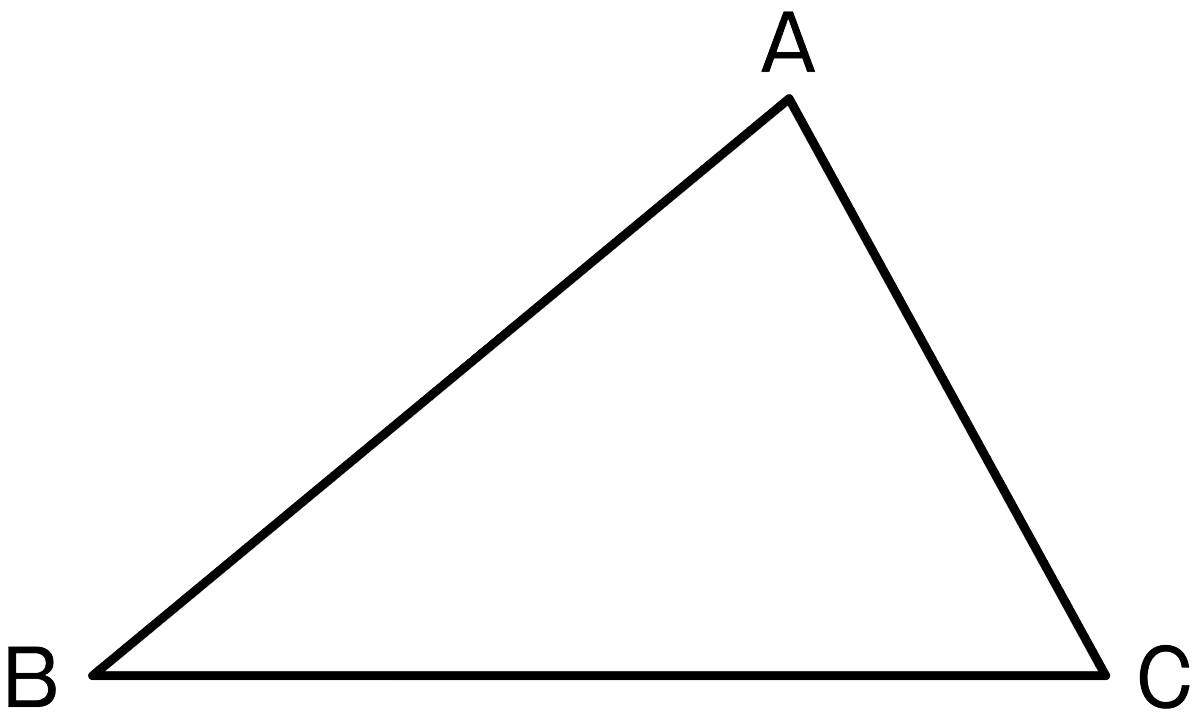
どうすれば合同な三角形をかくことができるでしょう。
辺の長さや、角の大きさを測ればいいと思います。
なるほど。辺は3本、角の大きさは3か所ありますね。いくつ調べればかくことができそうですか。
全部測る必要はなさそうだね。
いろいろなかき方があると思うので、それによって変わると思います。
では、今日は合同な三角形を書くための条件が見付かるとよいですね。
※ただ合同な図形をかくのではなく、「効率のよいかき方を考える」という本時の主眼を子供が理解するために、「すべての長さや角度を測る必要はない」ということを共有しておくことが大切です。
見通し
点Aの位置が決まれば、図形が決まる。
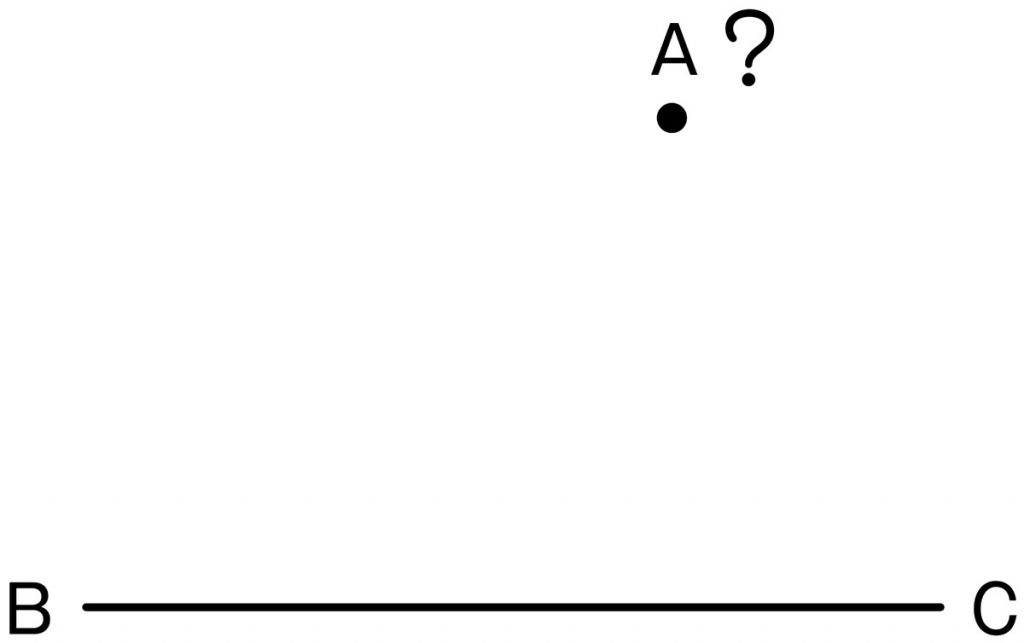
辺BCを一緒にかいてみましょう。合同な三角形をかくためには何が必要でしょうか。
点Aの位置を決めることです。
点Aの位置が決まると、合同な図形が決まりますね。
でも、どうすれば点Aの位置が決まるのかな。
点Aの位置の決め方について話し合い、合同な三角形をかくための条件をつくっていきましょう。
※図形が「決まる」という言葉は子供になじみがないため、「点Aの位置を探る」と活動のねらいを焦点化することによって、図形が決まるというイメージをもたせやすくなります。方法が一つとは限らないということも、子供たちと共有しておくとよいでしょう。

合同な三角形をかくための条件を考え、説明しよう。
自力解決の様子
A つまずいている子
辺の長さや角の大きさを測るが、点Aの位置を決めることができない。
B 素朴に解いている子
辺の長さや角の大きさを測り、コンパス、分度器、定規を使って、点Aの位置を決めることができている。
C ねらい通り解いている子
二辺とその間の角の長さや大きさを測定するなど、多様な方法で点Aの位置を決め、3つの要素で三角形が決まることに気付いている。
学び合いの計画
第三学年で二等辺三角形や正三角形の作図を、第四学年で一辺とその両端の角が与えられたときの三角形の作図を扱っていることから、本時では多くの子供が1つは考えをつくることができると思われます。本時では、自分が考えつかなかった方法に、触れることができるような交流を仕組むようにします。
イラスト/横井智美