小5算数「体積」指導アイデア《直方体・立方体の体積の求め方》
執筆/福岡教育大学附属久留米小学校教諭・藤木宏平
監修/文部科学省教科調査官・笠井健一
福岡教育大学教授・清水紀宏
単元の展開
第1時 体積の意味と単位を理解し、㎤のいくつ分の考えで体積を求める。
▼
第2時(本時)直方体、立方体の体積を計算で求める方法を考え、公式をまとめる。
▼
第3時 「㎥」の単位を知り、直方体の体積を求める。
▼
第4時 「㎥」と「㎤」の関係を理解する。
▼
第5・6時 複合図形の体積の求め方を考え、説明する。
▼
第7時 内のり、容積の意味を理解し、容積を求める。
▼
第8時 「㎥」と「l」、「㎤」と「l」の関係を理解するとともに、体積の単位の関係をまとめる。
▼
第9時 身の回りのものの体積や容積を求める。
本時のねらい
体積の単位や図形を構成する要素に着目し、直方体や立方体の体積の求め方を考え、公式に高めることができるようにする。
評価規準
直方体や立方体の体積を公式で求めることができる。(知識・技能)

ブロックを重ねて、いろいろな図形を作りました。どちらがどれだけ大きいか調べよう。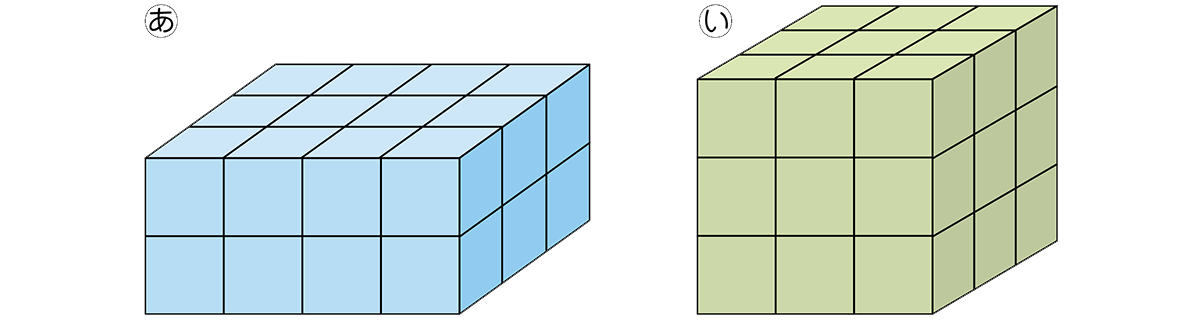

下の直方体や立方体の体積は、どちらが大きいでしょう。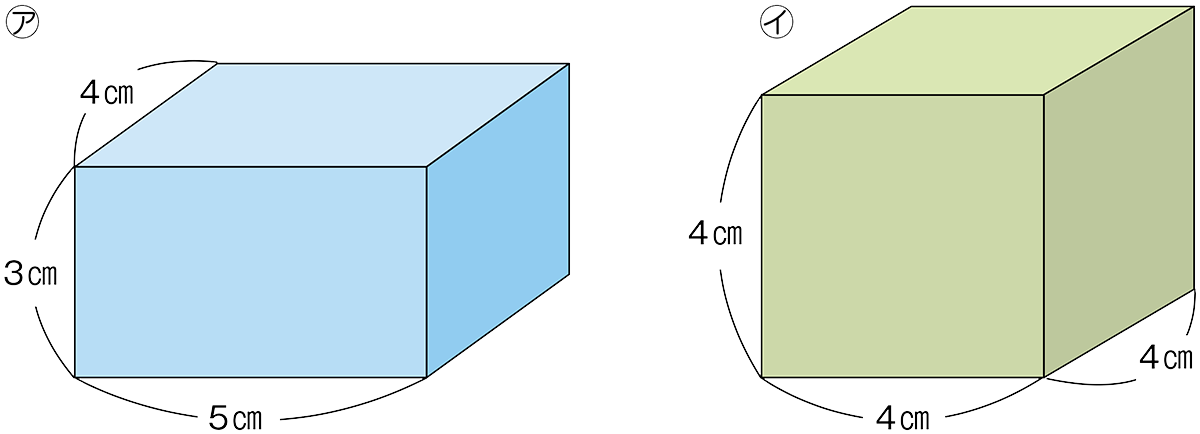
(前時問題場面と本時問題場面を提示した後)
前回との違いや同じところはなんですか。
ブロックで区切られていないところが違います。
辺の長さだけが分かっているところが違います。
体積で比べるところは同じです。
並べる数が多くて大変そう。
では今日は、どのようなめあてにしますか。

直方体や立方体の体積の求め方を調べよう。
見通し
- 1㎤のブロックに置き換える。(方法の見通し)
- 図形に線を引く。(方法の見通し)
- 計算する。(方法の見通し)
- 辺の長さ(着眼の見通し)
- 直方体のほうが少し大きそう。(結果の見通し)
自力解決の様子
A つまずいている子
・3つの面の面積で比べている。
㋐は、4×3+3×5+5×4=47
㋑は、4×4×3=48
だから㋑の体積が大きい。
・辺の長さを合計して比べている。
㋐は4+3+5=12
㋑は4×3=12
だから㋐と㋑の体積は同じ。
1㎤のいくつ分ではなく、面積や辺の長さの和で体積を捉えようとする。
B 素朴に解いている子
㋑のほうが4㎤大きい。
1㎤のいくつ分に着目し、その個数で体積を求めている。
C ねらい通り解いている子
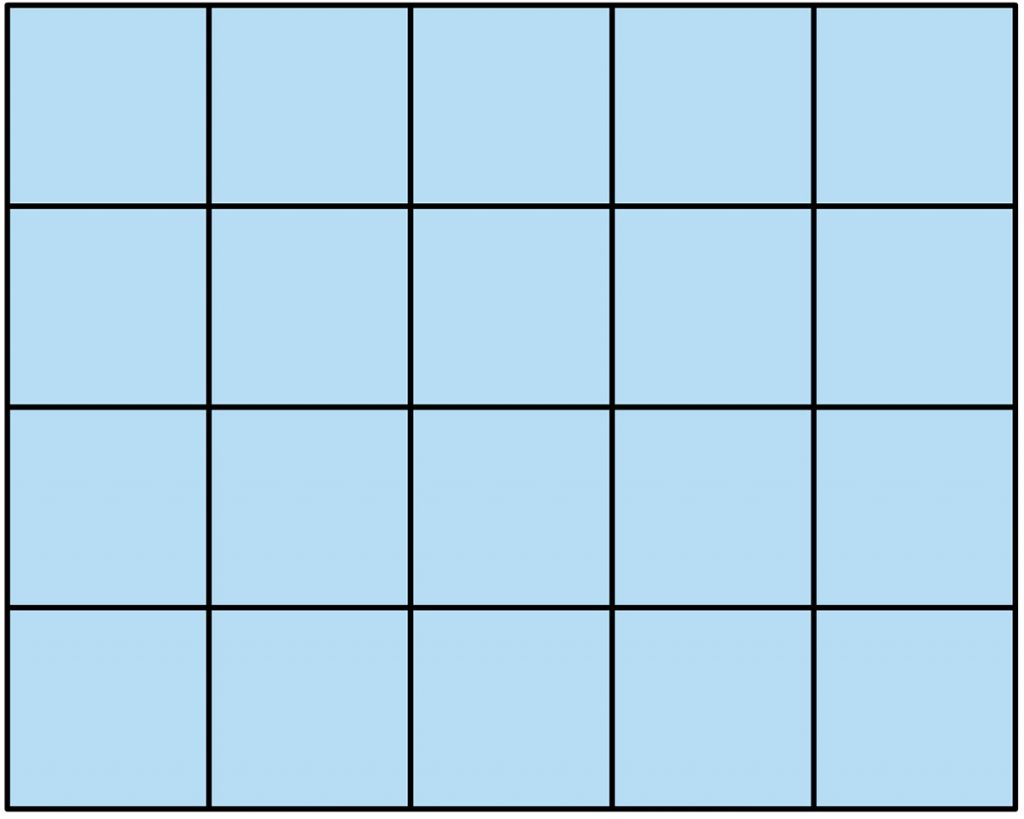
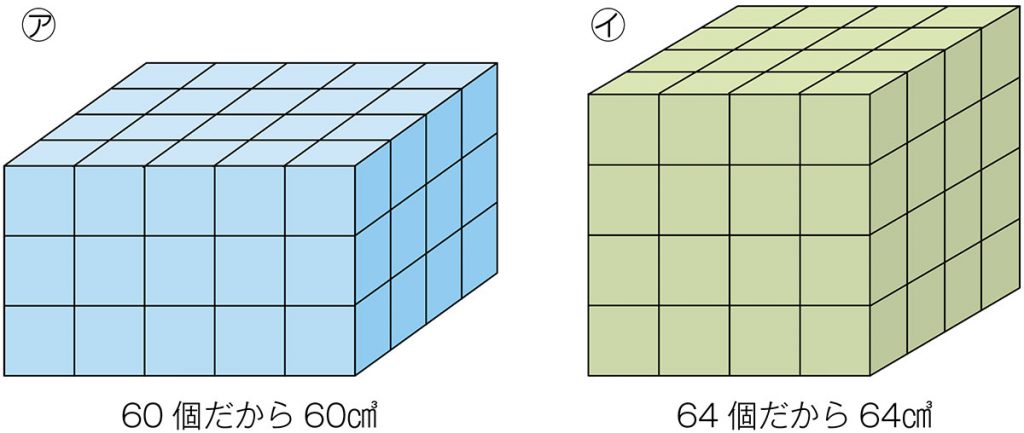
㋐1段目がたてに4個、横に5個並んでいるから
4×5=20
それが3段あるから
20×3=60
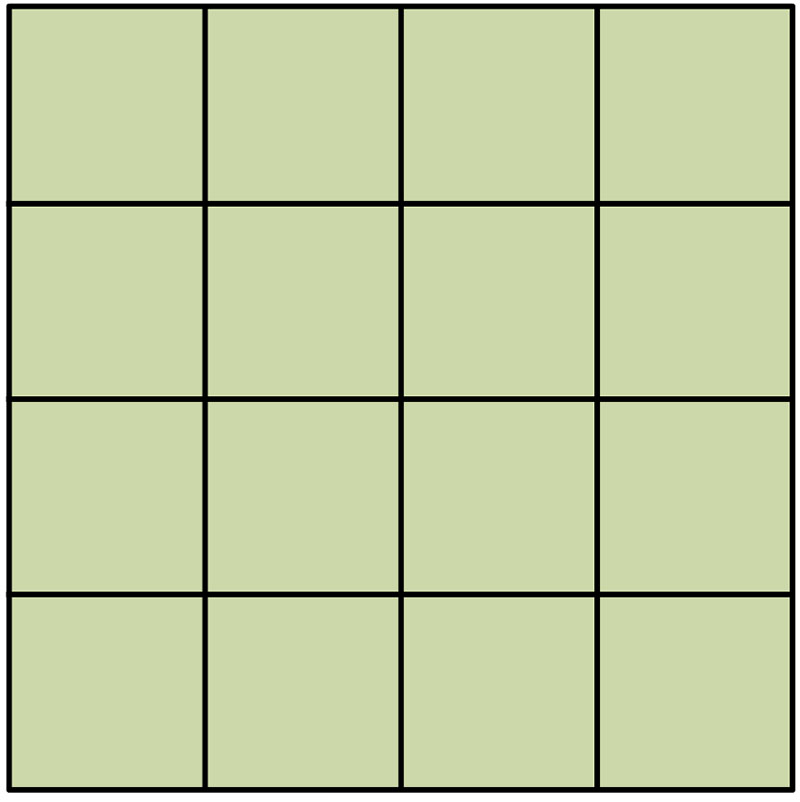
㋑1段目がたてに4個、横に4個並んでいるから
4×4=16
それが4段あるから
16×4=64
1段目の個数がなん段あるかに着目し、計算で体積を求めている。
学び合いの計画
自力解決の段階で、1人1台端末を活用して、自他の解決方法を共有しておき、互いの解決方法を見合うことができるようにしておきます。
イラスト/横井智美