小6算数「対称な図形」指導アイデア《線対称の図形の特徴》
執筆/新潟県新潟市立曽根小学校教諭・久道知弘
監修/文部科学省教科調査官・笠井健一
新潟県新潟市立新津第一小学校校長・間嶋 哲
単元の展開
第1時 折り紙で折られたさまざまな形を線対称の図形・点対称の図形・その他の形に分類する。
▼
第2時 線対称の図形の対称の軸を見付ける。
▼
第3時(本時)線対称の図形の構成要素と図形間の関係に着目し、線対称の図形を定義付ける。
▼
第4時 線対称の図形を作図する。
▼
第5時 点対称の図形を180度回転させ、ぴったり重なることを確かめる。
▼
第6時 点対称の図形の構成要素と図形間の関係に着目し、点対称の図形を定義付ける。
▼
第7時 点対称の図形を作図する。
▼
第8時 特別な多角形の対称性を調べる。
▼
第9時 正多角形の対称性を調べる。
▼
第10時 適用問題
▼
第11・12時 身の回りにある対称な図形を調べる・確かめる。
1人1台端末活用ポイント①
本単元でのタブレット型情報端末の利用は、主に単元導入と図形の作図で用いることができます。単元導入では、一度に複数の形を分類していきますが、これらの活動をタブレット型情報端末を利用しない場合、
①教師用のものを用意し、それらを子供たちとのかかわり合いのなかで分類する活動
②子供一人ひとりに複数の形を配付し、分類する活動
の2つが考えられますが、①の場合は複数の考えを取り上げることに限界があります。また、②の場合には準備に膨大な時間がかかります。そこで、タブレット型情報端末を利用することで、利点が3つあります。
A 準備の時間が減少する。
B 全員が操作できる。
C 操作したものを全体で共有でき、そこから交流を生むことができる。
ということです。
Cの全体での共有と交流については、タブレット型情報端末ならではのよさがあります。多くの考えに触れることができ、自分と友達の考えの違いから自然と交流が生まれ、内容も深まっていくことが期待できます。
さらに本単元では、ほかにも作図をする活動もあります。これらも「Geoboard」というアプリを利用することで容易に作成でき、また作成している様子を大型テレビなどに映すことで、作成のしかたも確認することができます。
本時のねらい
線対称の図形について、対称の軸と対応する点と点を結んだ直線が垂直に交わらない図形が線対称かどうかを考察することを通して、線対称の図形は対応する辺の長さ・角の大きさが等しく、対称の軸と対応する点を結んだ直線が垂直に交わる図形であることを理解することができる。
評価規準
線対称の図形かどうか、対応する辺の長さ・角の大きさ、対称の軸と対応する点を結んだ直線が垂直に交わっているかどうかを基に判断することができる。

線対称の図形の特徴を考えよう。
線対称とは、どんな図形のことでしたか。
線対称は、対称の軸を折り目に折ったら、ぴったり重なる図形です。
じゃあ、この図形は線対称の図形と言っていいでしょうか。
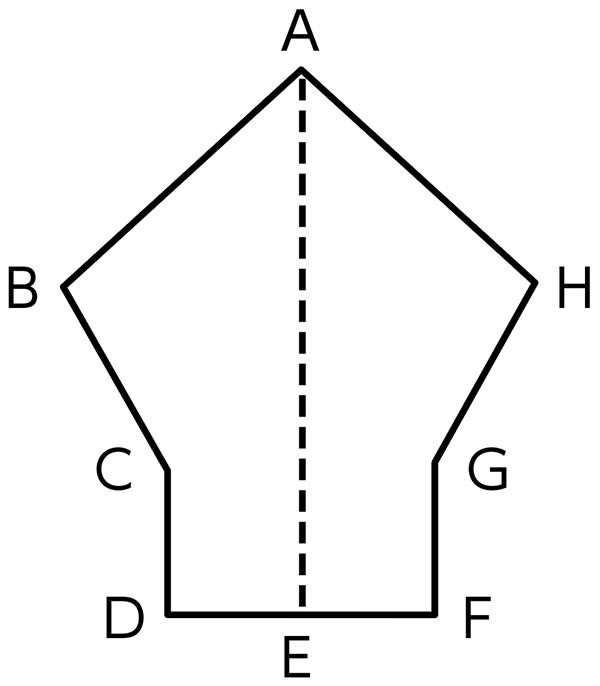
いいと思います。対称の軸で折ったら、ぴったり重なるからです。
どうしてぴったり重なるのでしょう。
だって、辺の長さが同じそうなところがあるからです。
角もそうです。
すごいですね。辺や角などに注目しているのですね。等しいところなんてあるのでしょうか。今からこの図形を配るので、探してみましょう。
線対称の図形はどんな図形と言ったらよいか、辺や角から秘密を探ろう。
辺ABと辺AHの長さが等しいです。
辺BCと辺HGも長さが等しいです。
角Bと角Hも大きさが等しいです。
角Dと角Fも大きさが等しいです。
例えば、みんなが言ってくれた辺ABと辺AHなどを「対応する辺」と言います。同じように角Bと角Hは「対応する角」と言います。また、点Bと点Hは「対応する点」と言います。これらを使ってまとめます。
線対称の図形とは、対応する辺の長さが等しく、対応する角の大きさが等しい図形。
線対称の図形の特徴は、ばっちり分かりましたね。では、これも線対称の図形ですよね。
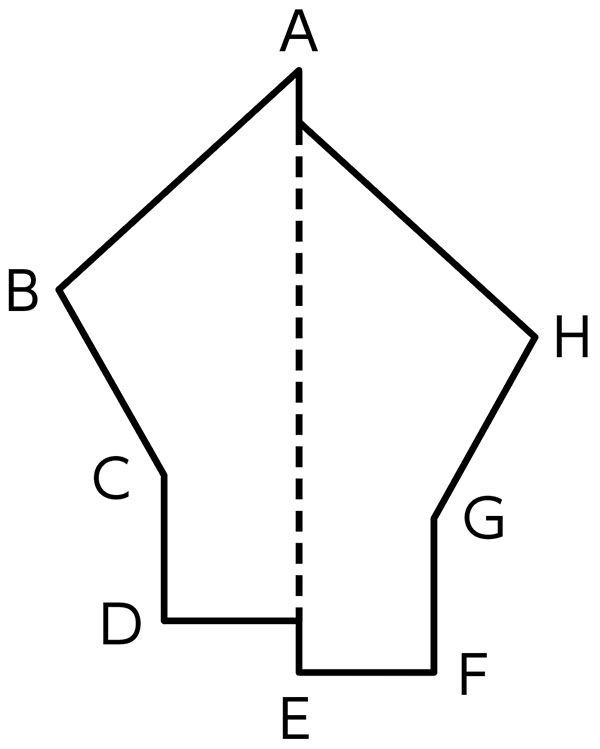
はい。だって、対応する辺の長さは等しいように見えます。
角度も等しいと思います。
実際に測ってみると、辺ABと辺AHはさっきと同じ長さですよ。角度も同様です。
でも、これっていいのかな。ぴったり折れないと思うんだけど……。

この図形は線対称の図形と言えるのかな。
見通し
この図形も配ります。さっきの図形と比べて、何が違うのでしょうか。
さっきの図形と比べて、対称の軸に対して右側の図形が少し下に下がっています。
なるほど。何か気付いたことがある人はいますか。
対称の軸と対応する点が関係していないかな。
自力解決の様子
A つまずいている子
辺の長さ・角の大きさが等しいため、線対称の図形と考えている。しかし実際に折ってみるとぴったり重ならないので、線対称かどうか分からない。
B 素朴に解いている子
実際に折ってみるとぴったり重ならないので、線対称の図形とは言えないことを理解している。
C ねらい通り解いている子
導入で考えた図形が対称の軸と対応する点を結んだ直線が垂直に交わっているのに対し、今回の図形が垂直に交わっていないことに気付いている。
学び合いの計画
折って重なる理由として、対応する辺の長さや対応する角の大きさが等しいことがよく挙がりますが、対称の軸とその他の構成要素の関係に着目した考えは、なかなか出ません。
イラスト/横井智美


