小4算数「分数」指導アイデア《1より大きい分数の表し方を考えよう》
執筆/新潟県公立小学校教諭・宮村徹
編集委員/文部科学省教科調査官・笠井健一、新潟県公立小学校校長・遠藤昇
目次
本時のねらい
本時1/9時
分数を使ったじゃんけんゲームを通して、分数には1より大きいものがあることを理解し、それらの表し方を考えることができる。
評価規準

じゃんけんゲームのルールを確かめるとともに、三年生までの既習事項の確認をする。その際に、図を用いて理解を深める。
見通し
例えば、どのようになると勝てますか。
チョキで1回、パーで1回勝つと、[MATH]\(\frac{2}{5}\)[/MATH]mと [MATH]\(\frac{3}{5}\)[/MATH]mを合わせて [MATH]\(\frac{5}{5}\)[/MATH]m、つまり1m進むので勝ちます。
図に表してみると、このようになりますね。
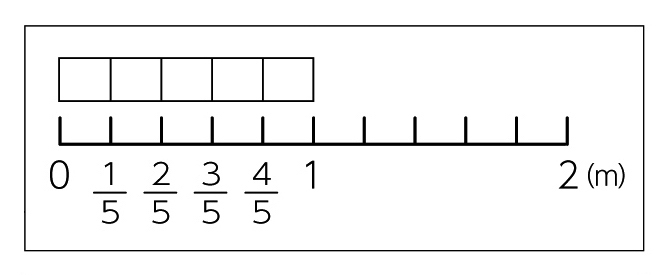
1mを超えてもいいんですか?
1mを超えるとは、どういうことですか?
例えば、パーで2回勝ったときとか……。
図では、どのように表せますか。
[MATH]\(\frac{3}{5}\)[/MATH]mと [MATH]\(\frac{3}{5}\)[/MATH]mで、1mより大きくなります。
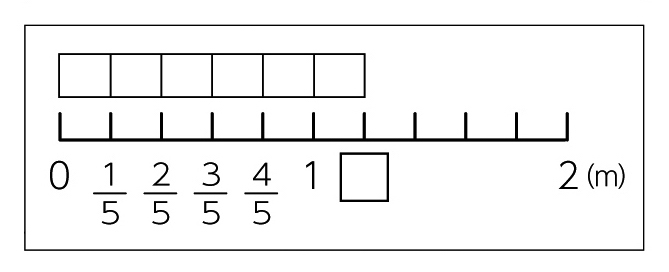
学習のねらい
1より大きい分数は,どのように表すとよいだろうか。
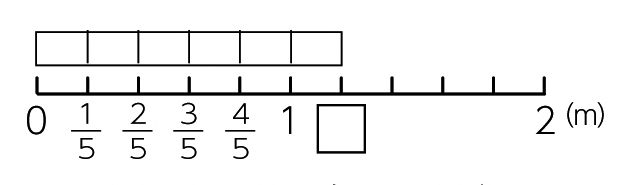
この図の長さは、何mと言えるでしょうか。
[MATH]\(\frac{6}{6}\)[/MATH]mじゃないかな。
答えが [MATH]\(\frac{6}{6}\)[/MATH]mだったら1mと同じになるからおかしいよ。
[MATH]\(\frac{1}{5}\)[/MATH]mが5つで1mになって、そこに [MATH]\(\frac{1}{5}\)[/MATH]mがもう一つあるから、やっぱり1mより長いね。
1mを5つに分けた1つ分の [MATH]\(\frac{1}{5}\)[/MATH]mが6つあるから、 [MATH]\(\frac{6}{5}\)[/MATH]mだと思うよ。
この図の長さは、 [MATH]\(\frac{1}{5}\)[/MATH]mが6つ分で [MATH]\(\frac{6}{5}\)[/MATH]m。または1mと [MATH]\(\frac{1}{5}\)[/MATH]mを合わせて1[MATH]\(\frac{1}{5}\)[/MATH]mと表します。 1[MATH]\(\frac{1}{5}\)[/MATH]mは [MATH]\(\frac{6}{5}\)[/MATH]mと同じ長さです。
「1mを5つに分けている」「[MATH]\(\frac{1}{5}\)[/MATH]mが5つ分で1m」のように、「1」を意識させて、単位分数のいくつ分という見方で分数の表し方を考えさせます。

自力解決の様子
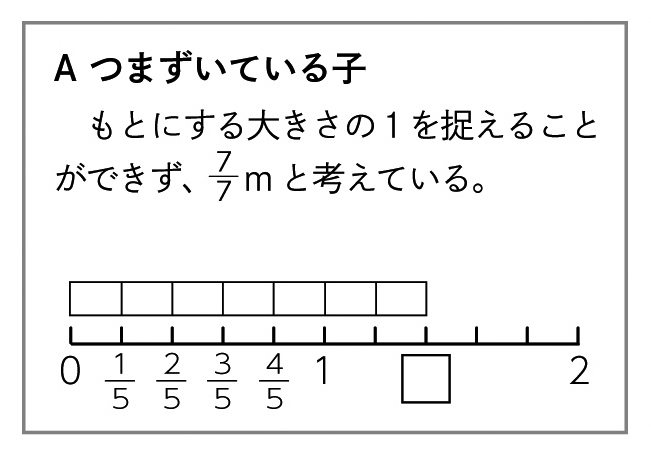
イラスト/横井智美
『教育技術 小三小四』2021年2月号より

