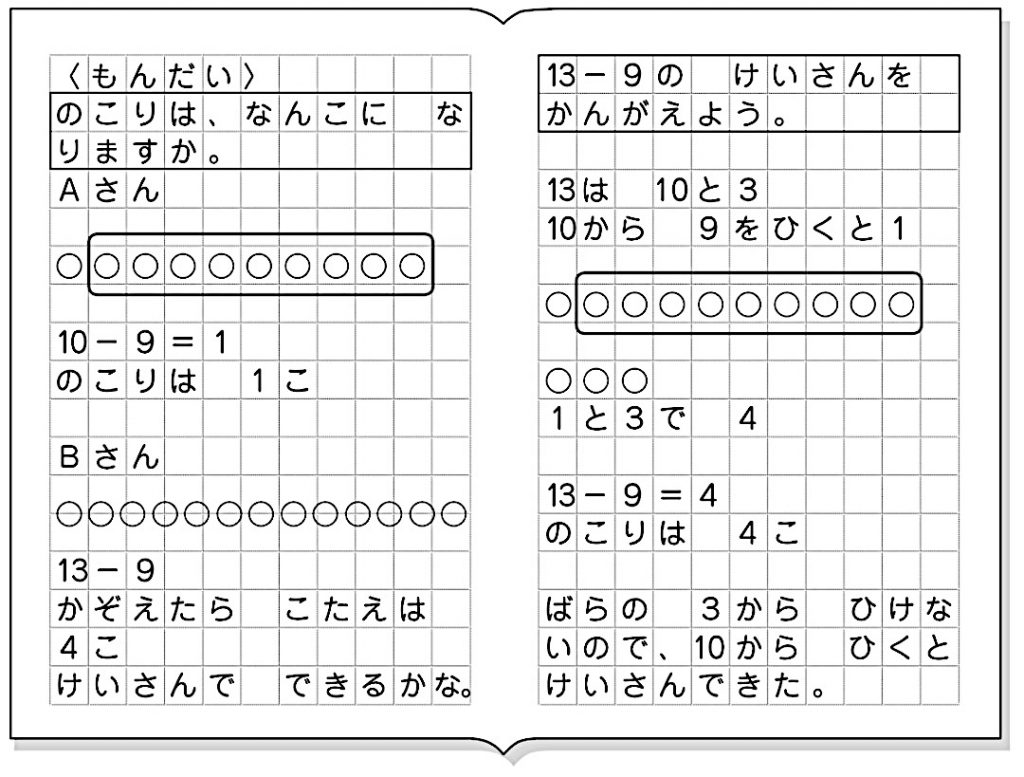
小1算数「ひきざん」指導アイデア(1/10時)《くり下がりのあるひき算のしかた》
執筆/神奈川県公立小学校教諭・能登谷亮
編集委員/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥
目次
本時のねらいと評価規準
(本時 1/10時)
ねらい
くり下がりのある減法計算のしかたについて、「10といくつ」という数の見方を基に、既習の計算を使って考えようとする。
評価規準
数の構成に着目し、くり下がりのある減法計算のしかたを、操作や図を用いて考え、表現しようとしている。

もんだい
どんぐりを9こつかいます。のこりはなんこになりますか。

Aさんは、何個になるかな。
10個あるね。9個使うから……。
ひき算をすれば分かるよ。
10-9になるね。残りは1個だ。
Bさんは、何個になるかな。
Aさんよりも、たくさんある。
全部で13個持っているよ。
13-9のひき算をすればいいね。
学習のねらい
13-9のけいさんは、どのようにかんがえればよいかな。
見通し
3から9は引けないね。 どこから9をとろうかな。
10-9の計算はできたよ。それが使えないかな。
自力解決の様子
A つまずいている子
13を10と3に分けられない。10を9と1とみることができない。
B 素朴に解いている子
13個のブロックから9個をとって、残りの4個を数えている。
C ねらい通りに解いている子
13を10と3に分けて、10のまとまりから9をとって、残りの1と3を合わせている。
学び合いの計画
13という数を、「10といくつ」と見ることができない子がいます。ここで大切なことは、「10とあといくつ」という数の見方を用いて、数を分解して引くことで、既習の計算が使えるようにするということです。そのために、10を「9と1」「7と3」「4と6」のように、「いくつといくつ」と見る力を十分に育てておく必要があります。
まず、13を10と3と見ることで、既習の「10は、いくつといくつ」が使えそうだということに気付かせていきましょう。ブロックの具体操作を通して、説明できるようにしていきます。
新たな計算に出合ったときに、既に知っている計算で求めることができるよう、数の見方を工夫して解決しようとする態度を養うことが重要です。
ノート例
全体発表とそれぞれの考えの関連付け
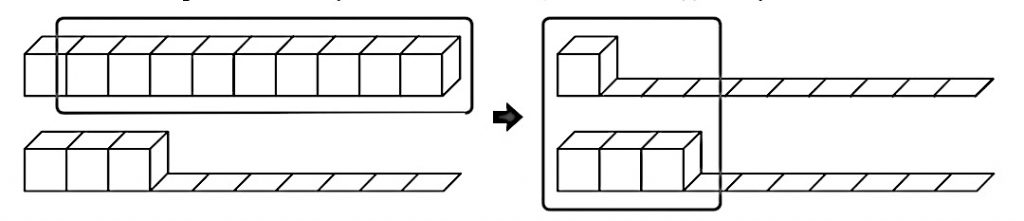
「10のまとまり」から9をとる。→残りの1と3を合わせる。
ブロックを使って13個から9個をとったら、残りは4個になりました。
13-2のときのように計算でできませんか。
13-2のときは3-2でできたけど……。
3-9はできません。
Aさんのとき、10-9はできたよね。
13を10と3に分けたらできそうだよ。
3から9は引けないけど、10からは引ける。
10-9の計算が使えそうということですか。
13を10と3に分けて、3はそのまま置いておけばよいです。
10から9を引いて1になります。さっきの3と合わせれば、残りは4です。
ブロックで数えなくても、10から引けば計算でできました。
「10といくつ」のやり方が使えたね。
評価問題
12-9のけいさんのしかたをいいましょう。
子供に期待する解答の具体例
12を10と2に分けます。10から9を引くと1です。1と2で3です。
本時の評価規準を達成した子供の具体の姿
「10といくつ」という数の見方を基に、くり下がりのある減法計算のしかたについて、操作や図を用いて考え、説明している。
感想例
- 10のまとまりから引くと、ばらから引けないときでも 計算することができました。
- 前に学習した、13を10と3に分けるやり方が使えたので、うれしかったです。
- 14とか15とか、もっと数が大きくなっても、同じ考え方でできそうです。
イラスト/松島りつこ・横井智美
「教育技術 小一小二」 2020年12月号より