小5算数「分数のたし算」指導アイデア《異分母の分数の通分を考えよう》
執筆／埼玉県公立小学校教諭・黒須直之
編集委員／文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
本時の位置5／12
ねらい
異分母の加法計算の方法を考えることができる。
評価規準
異分母の分数の加法計算の仕方について、分母を揃えることの意味を考え、説明している。（数学的な考え方）
問題場面
オレンジから絞ったジュースが15 Lと□Lあります。合わせて何Lになりますか。
児童の予想
式は、 15 ＋ 12 になりそうなんだけど…
※□にあてはめる数のカードとして、 15 、45 、 12 、13 、 34 を用意しておく。
【□の中に数のカード（ 15、 45 ）を当てはめながら、既習を確認して、本時の数値（ 12 ）を提示した後…】
これ、さっきまでと同じように計算できないよ。
どうしてですか?
だって、分母が違う数になっているもん。
これが今日の課題かな。
今までの学習との違いをはっきりさせることができましたね。では、今日のめあては何になりそうかな。
「分母が違う数のときの計算の仕方を考える」だと思います。
本時の学習のねらい
分母が違う数のときの計算の仕方を考えて、説明できるようにしよう。
見通し
分数を今まで習った小数になおして考えてみようかな。
分母が同じなら計算できるんだから、分母を同じにすることはできないかな。
15 + 12 なら、答えは、1Lの半分より多くなりそうだね。
自力解決の様子
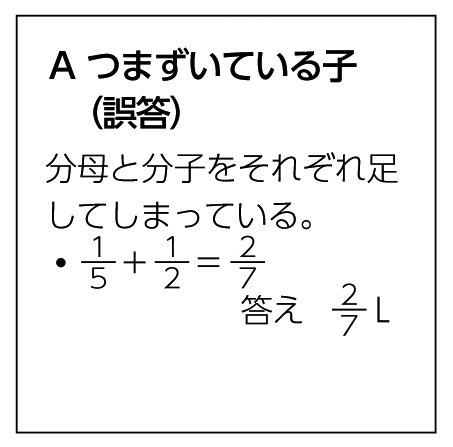
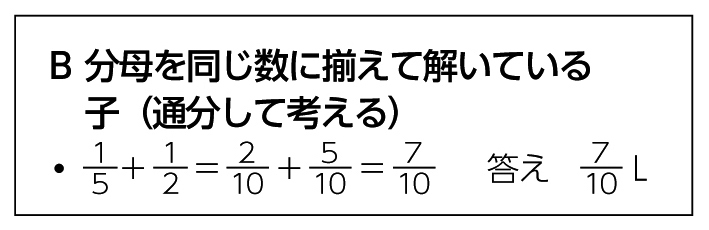
学び合いのポイント
本時では、異分母分数の加法の場面において、通分して分母を揃える知識・技能を具体的な場面に生かしていくことになります。そのため、学び合いで、異分母分数の計算の仕方を考えることに加えて、問題の場面と式や答えを関連付けていくことが大切になります。つまり、形式的に分母を揃えて計算するということに終始するのではなく、単位分数の何個分で考えるために通分するということを、話合いの中で導入場面の既習事項の確認と繋げながら、おさえていくことも大切になります。
イラスト／横井智美
『教育技術 小五小六』 2020年10月号より