小１算数「たしざん」指導アイデア（5/10時）《1位数どうしのくり上がりのあるたし算》
執筆/神奈川県公立小学校主幹教諭・純岡尚史
編集委員/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥
目次
本時のねらいと評価規準
(本時5/10時)
ねらい
1位数どうしのくり上がりのある加法計算で、被加数を分解して計算する方法(被加数分解)について考え、計算のしかたを説明することができる。
評価規準
10のまとまりをつくることに着目して、1位数どうしのくり上がりのある加法計算(被加数分解)のしかたを考え、ブロック操作と式を関連付けて説明している。
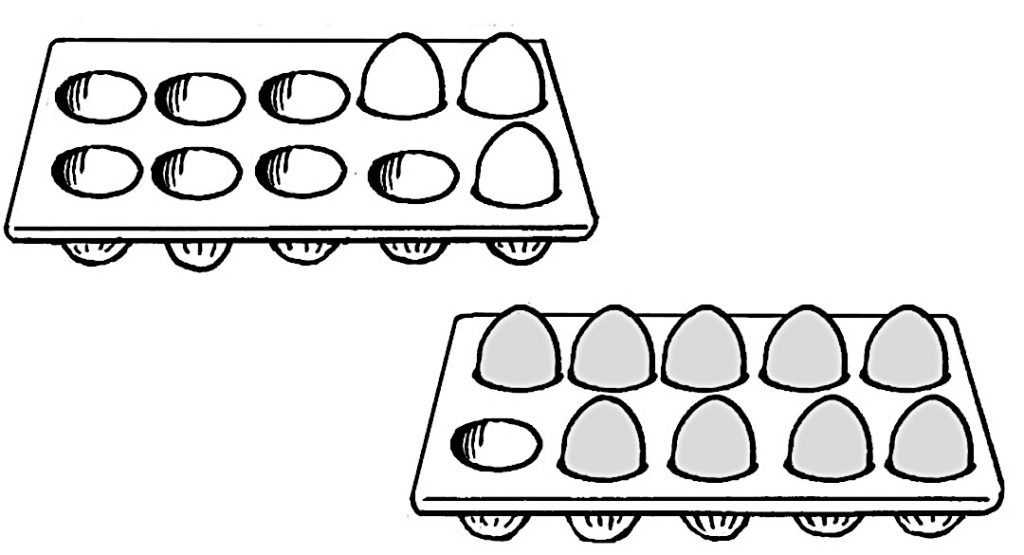
オムライスを作ろうと思っていたら、白色のたまごがあったのに、茶色のたまごパックを開けてしまいました……。
2つもパックがあると、じゃまになります。
合わせてしまえば、すっきりします。
(子供の言葉で、たし算になる文脈を描く)
もんだい
たまごは、あわせてなんこですか。 けいさんのしかたをかんがえましょう。
どんな式になりますか。
3+9になります。
どうしたら、答えが分かりますか。
これまでのように、ブロックを使うといいです。
学習のねらい
ブロックを動かして、計算のしかたを考えましょう。
見通し
これまでと同じように、ブロックで10のまとまりをつくればいいよ。【方法の見通し】
どちらのパックにもたまごを移すことができるね。【方法の見通し】
自力解決の様子
A つまずいている子
ブロック操作と式が結びついておらず、場面を理解できていない。
B 素朴に解いている子
10のまとまりを意識せずに、ブロックを数えながら12を求めている。
C ねらい通りに解いている子
「10のまとまりといくつ」という数の見方に着目して、10と2で、12と求めている。
学び合いの計画
新たな計算に出合ったときには、既習の見方・考え方を働かせて計算のしかたを求めることができるような授業展開を考えていくことが大切です。また、ブロック操作や式を関連付けることで、学習の理解が深まっていきます。
計算をふり返る場面では、ブロック操作と式を結び付けることで、被加数分解の場合には、小さい数を分解して10のまとまりをつくったほうが簡単なことを、実感をもって理解できるようにします。
簡潔・明瞭・的確、統合・発展的にふり返っていくことを繰り返し行い、経験させることができるようにしましょう。
ノート例
全体発表とそれぞれの考えの関連付け
C1(加数分解）
3はあと7で10だから、9を7と2に分けます。
10と2で答えは、12になります。
(答え) 12個
C2(被加数分解）
9はあと1で10だから、3を2と1に分けます。
10と2で答えは、12になります。
(答え) 12 個
合わせていくつになりましたか。
12個です。
本当ですか。ブロックを動かしてお話ししましょう。
C1:図参照(加数分解)
C2:図参照(被加数分解)
2人のやり方で、気付くことはありますか。
どちらも答えが、12個になっています。
C1さんは3を分けているけど、C2さんは9を分けています。
どちらも10のまとまりをつくっています。
どうして、そんなアイデアが浮かんだのですか。
大きい数は、10といくつで数えられるからです。
今回の場面では、どちらのほうがよいですか。
C2さんのほうが、ブロックを動かすのが楽です。
本時のまとめ
本時では、「10のまとまりといくつ」の見方に着目し、加数分解と被加数分解の計算のしかたを取り上げます。ブロック操作と式を関連付けていきながら、簡潔・明瞭・的確な視点でまとめていきます。
評価問題
どんぐりを、たかしさんは4こ、さちこさんは 8こひろいました。あわせてなんこになりますか。ブロックをつかって、 せつめいしましょう。
子供に期待する解答の具体例
8はあと2で10だから、4を2と2に分けます。10と2で12個です。
本時の評価規準を達成した子供の具体の姿
くり上がりのある加法の場面について、ブロックを用いて、答えの求め方を説明することができる。
感想例
- 10より大きいたし算には、前の数と後ろの数を分けてできることを知りました。
- 小さい数を分けたほうが、楽に計算できることが分かりました。
イラスト/松島りつこ・横井智美
『教育技術 小一小二』2020年10月号より
