小4算数「四角形を調べよう」指導アイデア《平行四辺形の定義や性質を利用して作図しよう》
執筆/新潟県公立小学校教諭・竹内直也
編集委員/文部科学省教科調査官・笠井健一、新潟県公立小学校校長・遠藤昇
目次
本時のねらい
本時10/15時
平行四辺形の作図について、一部分が破れた平行四辺形と同じ形の平行四辺形をつくる活動を通して、定義や性質を利用した平行四辺形のかき方が分かる。

評価規準
平行四辺形の定義や性質を利用して平行四辺形をかくことができる。
問題
右のように平行四辺形がやぶれてしまいました。この平行四辺形と同じ形を紙でつくりましょう。
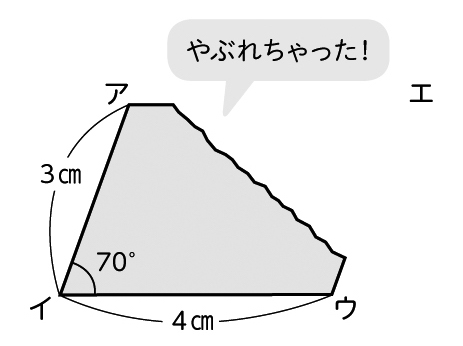
破れたところが分からないよ。かけるかなあ。
でも2本の辺の長さと1つの角の大きさは分かるよ。
頂点エはあのあたりだよね。頂点エの場所が分かれば、かけそうだよ。
学習のねらい
どうすれば、平行四辺形をかくことができるだろうか。
見通し
平行四辺形はどのような四角形でしたか。
【平行四辺形の特徴(定義や性質)】
①向かい合う2組の辺がそれぞれ平行
②向かい合う辺の長さが等しい
③向かい合う角の大きさが等しい
④となり合う角の大きさの和が180°
前時までに学習した平行四辺形の定義や性質を想起させ、作図の方法を考える見通しをもたせます。
平行な直線をかけばいいのかなぁ。
辺の長さや角の大きさが等しいことも使えそうだね。
どれか一つの特徴を使えばできそうだよ。
自力解決の様子
A つまずいている子
定義や性質は想起したものの、それらをどう利用すればよいか分からない。
B 素朴に解いている子
定義や性質を想起しつつも、定規を使って半ば直感的に作図している。
C ねらい通り解いている子
利用する定義や性質を意識し論理的に考えながら、コンパスや三角定規を使って作図している。
学び合いの計画
イラスト/横井智美
『教育技術 小三小四』2020年7/8月号より

