小6算数「分数×分数」：数直線・面積図・関係図で攻略①【動画】

【トモ先生の算数チャンネル】第5回

小学校の算数の授業づくりをお手伝いする『トモ先生の算数チャンネル』。いよいよ具体的な授業づくりに役立つポイントの紹介が始まります！　今回は、6年生の「数と計算／分数×分数」編。トモ先生が、学習指導要領を紐解きながら解説します。

このシリーズでは、小学校高学年の算数を専門とする髙橋朋彦先生が、小ネタや道具に頼らずに、基本を大切にした質の高い授業づくりができるアイデアをお届けしていきます。

分数の学習で大切なこと

学習指導要領、読んでいますか？　⋯なかなか読む時間を取るのは難しいですよね。そこで、算数チャンネルでは、私が読み込んだ学習指導要領のポイントをみなさんにお伝えしていきたいと思います。

さて、6年生の分数×分数ですが、学習指導要領解説算数編（H29年6月告示）にはこのように書かれています。

〔算数的活動〕（1）
ア　分数についての計算の意味や計算の仕方を、言葉、数、式、図、数直線を用いて考え、説明する活動

小学校学習指導要領解説 算数編（H29年6月告示）より

分数×分数の学習は、どうしても「計算が正確にできるか」に重きを置きがちです。

もちろん、正確に計算できることは大事なことですが、「なぜその計算になるのか？」ということを、図を使いながら考え、説明できるようになることが大切です。

3つの図を理解しよう！

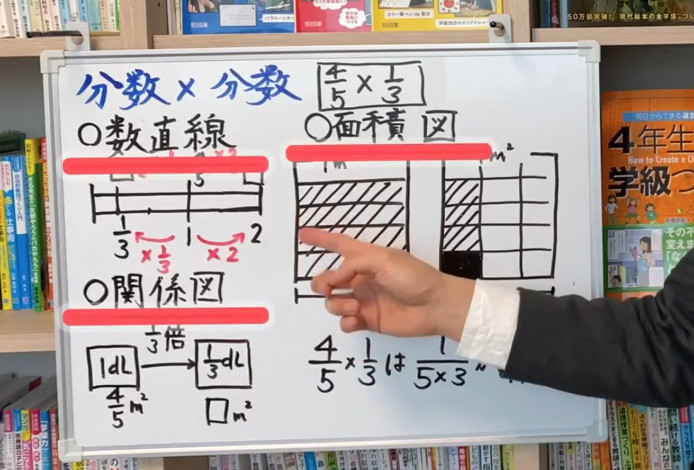
数直線・面積図・関係図――この3つの図には、それぞれ別の角度で理解を深める特徴があります。

【問題】
1dLで[MATH]\(\frac{4}{5}\)[/MATH]㎡塗れるペンキがあります。このペンキ[MATH]\(\frac{1}{3}\)[/MATH]dLでは何㎡塗れますか？

この問題を例にして、一つずつ見ていきましょう！

1. 数直線：割合で考える