小4算数「式と計算」指導アイデア
執筆／埼玉県公立小学校教諭・鈴木智史
編集委員／文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
本時の位置 5/8時
分配法則を用いた計算方法の工夫
ねらい
分配法則を□や○などを使って一般的にまとめたり、それを用いて計算を簡単に行う工夫を考えたりすることを通して、分配法則についての理解を深める。
評価規準
分配法則について理解している。（知識理解）
問題
○と●は全部で何こあるでしょう。
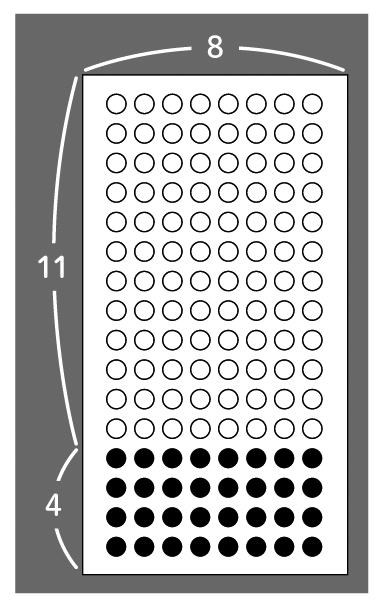
アレイ図を見て、何か気付いたことはありますか。
縦が2色の丸に分かれています。
○と●が合わさって、1つの図になっています。
アレイ図の場面を式に表して考えたことはありませんでしたか。
2年生のときのかけ算でも、アレイ図を使ってかけ算の式に表して考えました。
アレイ図の場面を式に表すことは学習してきていますね。アレイ図を使い、丸の数を工夫して求めましょう。
学習のねらい
アレイ図を使い、工夫して計算しましょう。
見通し
○と●の部分を、それぞれ分けて求めて、たせばいいと思います。
縦の15を10と5に分けて計算すればいいと思います。
11と4をたして15にすれば、一度にできると思います。
自力解決
A つまずいている子
アレイ図のどこに着目して考えればよいか分からない。
B 素朴に解いている子
アレイ図の表す場面を理解し、計算のしかたを説明している。
C ねらい通り解いている子
工夫して計算し、図と式を関連付けて説明している。
学び合いのポイント
イラスト／小沢ヨマ
『教育技術 小三小四』 2019年10月号より
