小2算数「かけ算(1)」指導アイデア《かけ算のしきになるばめんを見つけましょう》
執筆/福岡県公立小学校教諭・阿部万優子
編集委員/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
本時のねらいと評価規準
[本時4 /25時]
ねらい
乗法の意味(一つ分の大きさが決まっているときに、その幾つ分かに当たる大きさを求める場合に用いられる)について理解する。
評価規準
乗法が用いられる場面を具体物や図を用いて考え、式や言葉で表すことができる。[知識・理解]

問題場面
ゆうえんちのえから、かけ算のしきになるばめんを見つけましょう。
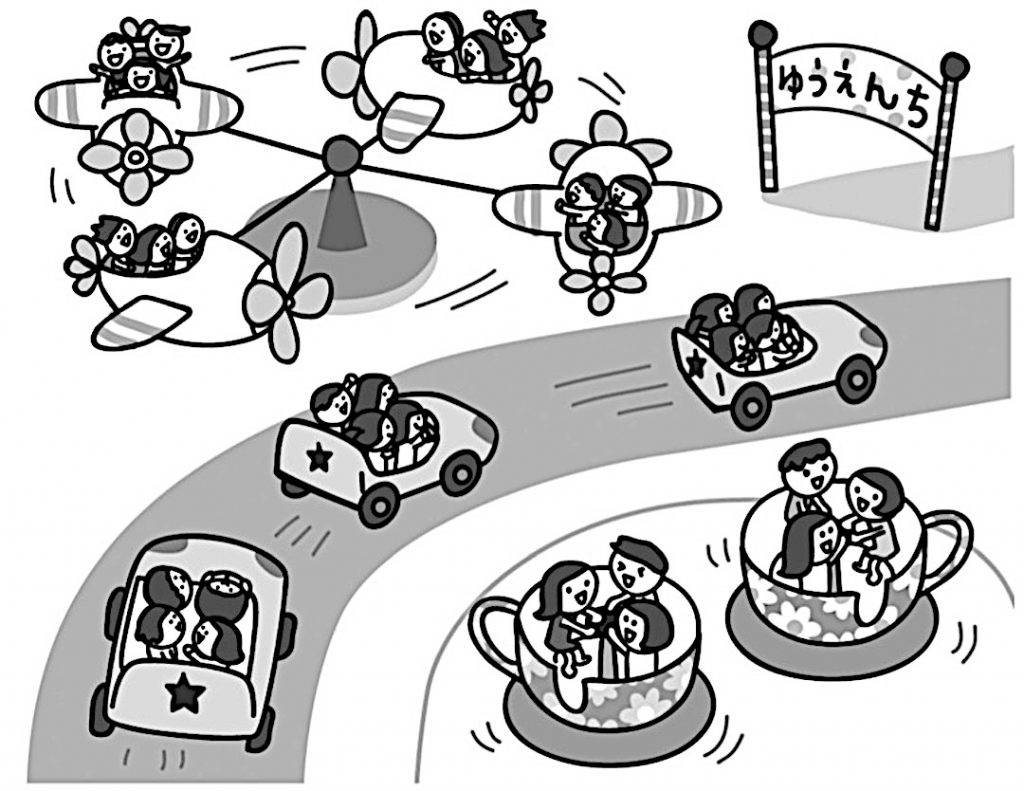
今日は、前の時間に学習したかけ算を見付けましょう。
かけ算は、どんなときに使えますか?
この絵のように、1台のコーヒーカップに3人ずつ乗っていて、2台あるときだと思います。
前の時間に出て来たように、2人乗りの自転車に2人ずつ乗っていて、6台あるときだと思います。

そうですね。(前の学習に使った自転車の絵を見せて)2人ずつ6台分で12のように、1つ分の数が何個あるかで、全部の数を表すときに使えますね。コーヒーカップの他にもかけ算になる場面を、遊園地の絵から見付けてみましょう。
本時の学習のねらい
かけ算のしきになるばめんを見つけて、ブロックやしきやことばであらわそう。
子どもたちに、ブロックを使って表すよう指示をします。遊園地の絵からかけ算に表すことができる絵を見付けたら、その場面をブロックで表した後に、かけ算の式を書かせます。式で表した後に、「〇人ずつ〇個だから、全部で〇人」のように、 意味を言葉で説明するよう促します。
見通し
1つ分に同じ数ずつ乗っているものを見付ける。
自力解決の様子
A つまずいている子
1台ごとに同じ人数ずつ乗っている乗り物を見付けられない。または、見付けていてもブロックで表していない(挿絵に〇を付けるなど)。

B 素朴に解いている子
1台ごとに同じ人数ずつ乗っている乗り物を見付け、ブロックとかけ算の式で表しているが、意味の説明ができない。

C ねらい通りに解いている子
1台ごとに同じ人数ずつ乗っている乗り物を見付け、ブロックとかけ算の式で表し、その意味を言葉で書いている。

学び合いのポイント
子どもたちは、かけ算( 1 )の1時間目の学習で、いろいろな乗り物の人数を調べ、「1台に何人ずつで何台分ある」という人数の表し方を学習しています。本時の学習では、その学習を生かして、かけ算の式に表すことを考えていきます。Aの子どもについては、全体交流前に個別に指導を行い、自力解決ができるようにしましょう。
イラスト・コダシマアコ 横井智美
『教育技術 小一小二』2019年10月号より

