つまずきがちな「小数の割り算」が断然面白くなる授業のコツ3つ

授業中、子供たちの表情に「？」マークが浮かんでいるのに、軌道修正できずにそのまま続行…。そんな苦い経験もこれで解消！　つまずきがちな「小数の割り算」が断然面白くなる、スペシャリストによる授業のコツをマスターしましょう。

執筆／富山県公立小学校教諭･前田正秀

つまずき1「2.5等分って、どういうこと？」

ポイントは、意味の理解

計算の指導において、「計算の方法（どうやって答えを出すか）」については、丁寧に指導されることが多いのですが、「計算の意味（なぜ、その式になるのか）」については、指導がおろそかになりがちです。

しかし、この単元は、意味の理解にこそ、大きなつまずきが潜んでいます。

これまでの整数のわり算では、例えば
「2ｍで300円のリボン、1ｍの値段」の300÷2なら、300円の2等分と考えることができました。しかし、「2.5ｍで300円のリボン、1ｍの値段」の300÷2.5は、2.5等分 という説明では意味が通じません。

そこで、わり算の意味を「300を2.5と見たときの1当たりの大きさを求める計算」という意味に拡張する必要が出てきます。単位量を求める計算という意味を理解するのが、子供にとっては難しいのです。

まずは感覚で理解

わり算の意味は、丁寧に説明し過ぎると、かえって理解しづらくなります。最初のうちは、ハードルを低くし、感覚的に理解させたほうがよいと思います。

例えば「リボンを □ｍ買いました。代金は300円でした。1ｍの値段は何円ですか」という問題を提示し、「□の中がどんな数なら簡単に解けますか」と尋ねます。子供からは「3」「2」といった答えが返ってくるでしょう。

3ｍなら300÷3で100円
2ｍなら300÷2で150円

言葉の式で表せば、「代金÷買った長さ」となります。

ここで、「ちょっと意地悪をするよ」と言って、教師が□の中に2.5を入れます。こうして、整数の場合を例にすることで、子供が感覚的に300÷2.5という式を導き出すことができます。

図を使って確実に理解

もちろん、ここでは、式を立てさえすればよいわけではありません。大切なのは、式を立てた後で、わり算には「1当たりを求める計算」という意味もあることをしっかり確認することです。

今回の300÷2.5というわり算は、300を2.5と見た時の1当たりを求める計算になっています。割る数が1より大きいうちは、感覚的に式を立てることもできますが、ここでわり算の意味を理解しておかないと、後々苦労します。

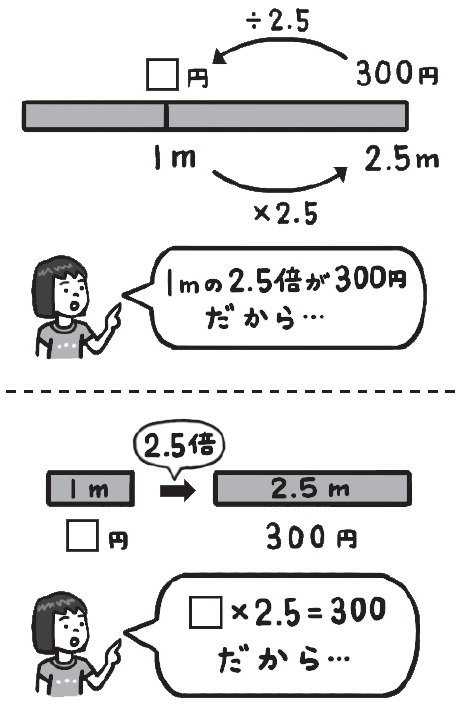
教科書では数直線図で説明されていることが多いですが、テープ図や関係図を併用するのもよいでしょう。さらに確実な定着を図ることができます。それらの図を使って、子供に300÷2.5の式になる理由を説明させると効果的です。

つまずき2「割ったのに大きくなるの？」

ポイントは、「1当たり」のイメージ

わり算の意味理解において、最大のつまずき。それは、「120÷0.8」といったように割る数が1より小さい計算です。わり算は「等分する計算」と思い込んでいる子にとっては、0.8で割るというイメージがもてません。ここで、わり算は「1当たりの大きさを求める計算」という理解が生きてくるのです。

また、答えの大きさもつまずきの原因になります。子供にとって、これまでは、割れば必ず答えが小さくなりました。割ったのに答えが大きくなるというのは、理解し難いものです。ここでも「120を0.8と見たときの1当たりを求める計算」という理解があれば、答えが120より大きくなることをイメージしやすくなります。

割る数と答えの関係に着目

授業では、答えの大きさに着目させたいものです。例えば、導入で用いたリボンを提示し、「1ｍでは120円でしたね」と確認します。その上で、別のリボンを提示し、「このリボンはね…」と言いながら、「□ｍで120円」と板書します。

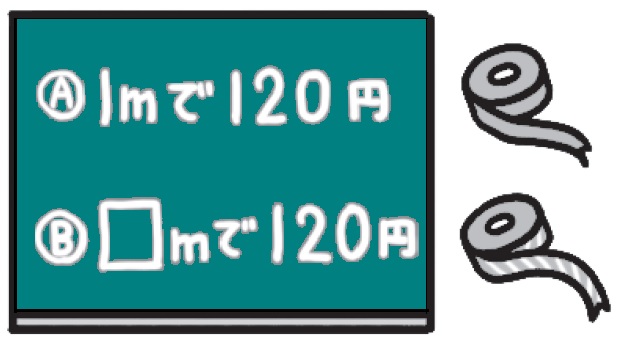
子供は、「前のリボンより安いよ」「そうとは限らないよ。だって…」と、1ｍ当たりの値段の大きさに着目していくことでしょう。

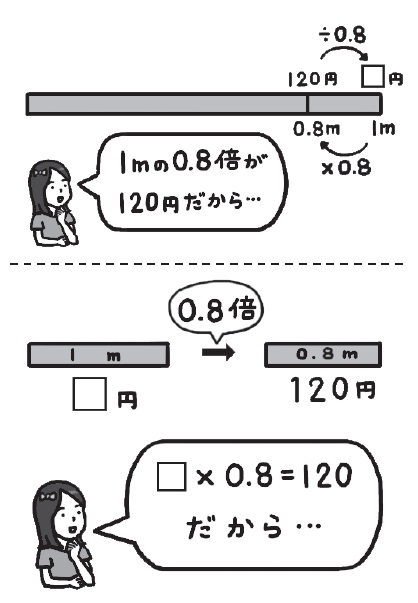
前述した導入の提示と同様に、整数の場合を例に出して、1ｍ当たりを求める式を立てます。□が3ｍなら120÷3、2ｍなら120÷2ですから、0.8ｍなら120÷0.8という式になります。

子供なりの言葉で説明

式が立ったら、答えを求める前に、まず120円より大きくなるか小さくなるか、見当をつけさせるとよいでしょう。そして、そう思った理由を語らせます。

▼子供たちの考え

子供なりの言葉で説明し合うことで、周りの子供たちもイメージしやすくなります。

どんなに丁寧に説明しても、やっぱり意味が分からないという子もいます。1度の授業で全てを理解させようと気負いすぎず、継続的にくり返し指導していく根気と覚悟が必要です。

つまずき3「また、うっかりミスしちゃった」

イラスト／宇和島太郎

『小五教育技術』2018年6月号より