小6算数「分数のわり算」指導アイデア
執筆／神奈川県公立小学校主幹教諭・元田光二
編集委員／文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥
目次
本時のねらいと評価規準
(本時 2/11時 分数÷分数の計算の仕方)
ねらい
除数が分数の場合の計算の仕方を、数直線を用いたり、除法の性質を生かしたりして根拠を明らかにしながら説明する。
評価規準
分数÷分数の計算の仕方を、既習の計算方法と関連付けて考えたり、図を用いて考えたりすることができる。
問題１
[MATH]\(\frac{2}{3}\)[/MATH] dLのペンキで、 [MATH]\(\frac{4}{9}\)[/MATH] m²ぬれました。このペンキ1dLでは、何m²ぬれますか。
どんな式になりますか。
昨日の問題と同じで、1dLを求めている。
式は、[MATH]\(\frac{4}{9}\)[/MATH]÷[MATH]\(\frac{2}{3}\)[/MATH]です。
分数×分数の計算は、分子と分母をそれぞれかけて求めることができたので、同じように考えてみよう。
[MATH]\(\frac{4÷2}{9÷3}\)[/MATH]=[MATH]\(\frac{2}{3}\)[/MATH]
分数÷分数も同じように、分子同士と分母同士をそれぞれをわれば、できるね。
この方法は、いつでもできますか。
お互いに、わり切れない場合はできない。計算が
2÷3になったら、できないな。
分数÷分数は、できないこともあるのかな。
計算の仕方を、考えてみたいな。
問題２
[MATH]\(\frac{3}{4}\)[/MATH]dLのペンキで、 [MATH]\(\frac{2}{3}\)[/MATH]m²ぬれました。このペンキ1dLでは、何m²ぬれますか。
式は、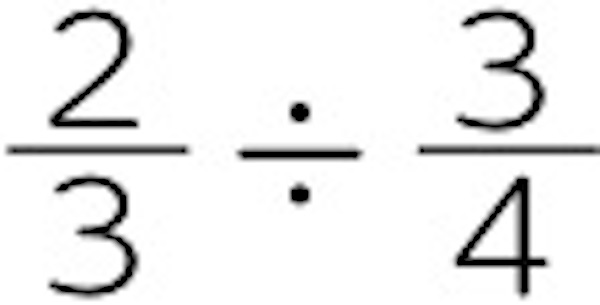
です。
さっきの方法と同じように、考えてみよう。
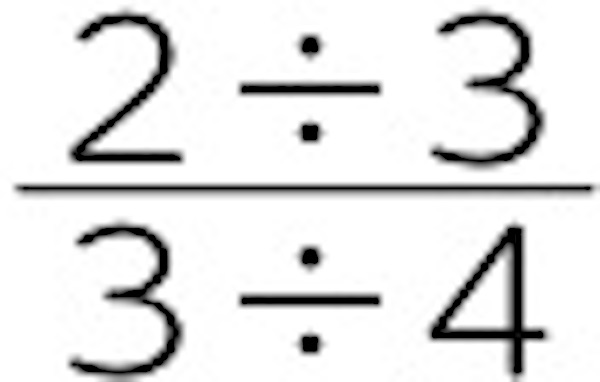。これだと2÷3がわり切れないので、できない。
これまで習った計算の形にできれば、できそうだ。
これまでに、どんな計算を習いましたか。
小数÷小数 分数×分数 分数÷整数です。
[MATH]\(\frac{2}{3}\)[/MATH]は小数にできないから分数×分数にしたり、分数÷整数にしたりしてみよう。
分数×分数のときに数直線を使って考えたけれど、同じようにできるのかな。
これまでに習った計算で考えたり、数直線を使ったりして考えてみましょう。
本時の学習のねらい
分数÷分数の計算の仕方を考えよう。 ～[MATH]\(\frac{2}{3}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]は、いくつだろう～
見通し
わる数の[MATH]\(\frac{3}{4}\)[/MATH]が整数になれば、分数÷整数になるので計算できそうだ。
[MATH]\(\frac{1}{4}\)[/MATH]dLでぬれる面積を求めてから、1dLにしたら求められるかな。
自己解決
A つまずいている子
既習の計算を基に考えたり、数直線を活用したりすることができず、計算ができない。
B 素朴に解いている子
除法の性質を使って、[MATH]\(\frac{3}{4}\)[/MATH]に×4をして分数÷整数で考える。
C ねらい通りに解いている子
わる数を1にすることに着目して、 [MATH]\(\frac{3}{4}\)[/MATH]に逆数をかけ、÷1の形に直して考える。
学び合いの計画
本単元は、小学校の計算領域の最終単元であり、四則計算のまとめを図る単元でもあります。これまで、どのような学習をしてきたか、子供が既習内容をどの程度身に付けているかを、教師はしっかりと把握し、授業にあたることが大切です。
イラスト／斉木のりこ 横井智美
『教育技術 小五小六』2019年6月号より
