小4算数「小数のかけ算とわり算」指導アイデア《余りがある場合の小数÷整数の筆算の仕方について考える》

執筆/東京都港区立御田小学校指導教諭・沖野谷英貞
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、東京都板橋区立上板橋小学校副校長・内藤信義
目次
年間指導計画
・大きい数
・折れ線グラフ
・角とその大きさ
・わり算1桁
・小数のしくみ
・垂直・平行と四角形
・わり算2桁
・およその数、計算の見積もり
・そろばん
・倍の見方
・資料の整理
・式と計算
・変わり方
・面積
・分数
・小数のかけ算とわり算
・直方体と立方体
単元の展開(各時の主な学習活動内容)
第1時 数の構成やかけ算の性質に着目し、小数×1桁の数(0.2×7など)の計算の仕方を考える。
第2時 数の構成やかけ算の性質を基にして、小数×1桁の数(2.3×7など)の立式とその計算の意味について考える。
第3時 前時で学習した小数×1桁の数の計算の意味や整数×整数の筆算の仕方を基にして、小数×1桁の数の筆算(2.3×7など)の仕方について考える。
第4時 小数×2桁の数の筆算(2.7×12など)の仕方を理解し、その計算ができるようになる。
第5時 小数の範囲を広げて、[MATH]\(\frac{1}{100}\)[/MATH]の計算(2.38×4など)や積に空位のある計算(4.05×36など)の筆算ができるようになる。
第6時 数の構成に着目し、小数÷1桁の数の計算(0.6÷3など)の仕方を考える。
第7時 小数÷1桁の数(7.2÷3など)の立式と、その計算の意味について考える。
第8時 小数÷1桁の数の計算の意味や整数÷整数の筆算の仕方を基にして、小数÷1桁の数の筆算(7.2÷3など、一の位に商あり、余りなし)の仕方について考える。
第9時 小数÷1桁の数の範囲を「一の位に商が立たない場合(4.9÷7、4.92÷6など)」に広げて、筆算の仕方を理解し、その計算ができるようになる。
第10時 小数÷2桁の数の筆算(64.8÷36、7.74÷43など)の仕方を理解し、その計算ができるようになる。
第11時(本時)余りがある場合の小数÷整数の筆算(16.4÷3など)の仕方について考える。
第12時 小数÷整数(15.6÷8など)で割り進みをするときの筆算の仕方を理解し、その計算ができるようになる。
第13時 整数÷整数(2÷3など)で割り進み、割り切れない場合の商の概数処理について理解する。
第14時 小数が何倍かを表すのに用いられることを、倍の計算を基に考える。
第15時 学習内容の定着を確認し、理解を確実にする。
本時のねらい
小数÷整数の余りを求める計算において、除数と余りの関係に着目し、余りの大きさを正しく捉え、計算することができる。
評価規準
16.4÷3の余りの大きさについて、確かめの式やテープ図を用いながら、除数と余りの大小関係を根拠に説明している。
本時の教材のポイント
これまで、小数÷整数の余りのない場合について、計算の意味や筆算の仕方を学習してきました。本時では、余りがある場合の問題を扱います。その際、子供たちが「余りの表し方」や「余りの大きさ」に迷う姿が見られます。16.4÷3の計算では、商を5とした後に、「14」と「1.4」の2通りの余りが出ることが予想されます。そして、この余りが2通り出ることを生かして「余りは割る数より小さい」という関係に着目しながら、余りの大きさを考えていくことをねらいとします。これは、第3学年「余りのあるわり算」で学習した「割る数と余りの関係」が小数にも成り立つかを考える学習とも言えます。
余りの大きさを考える際には、「割られる数の小数点に揃える」といった形式的な指導にとどめず、商と余りの関係を「除数×商+余り=被除数」の確かめの式やテープ図で確認することを通して、余りの小数点の位置とつなげていくことが大切です。
本時の展開
これまで小数のわり算の学習をしてきましたが、小数÷整数ならどんな計算でもできそうですか。
はい。でも、今までは全部割り切れていたので、余りがないわり算でした。
小数÷整数の計算にも、余りがあるわり算があるんじゃないかな。
どうして、そう思ったんですか。
整数÷整数は余りがあるわり算があったから、小数÷整数も余りがあるわり算があると思いました。
整数のわり算と小数のわり算を関連付けて考えるところが素晴らしいですね。では、今日も小数÷整数の問題を考えていきましょう。

16.4mのリボンがあります。リボンを3mずつ切って、花かざりを作ります。3mのリボンは何本作れて、何mあまりますか。
これまでの問題と違うところはありますか。
「何m余りますか」と問題文に入っているから、今日の問題は余りがあります。
16.4mは小数だから、3mずつリボンを切ると、余りが出そうだなと思いました。
計算をする前に見当をつけることは大切ですね。式はどのようになりそうですか。
16.4÷3です。
3mのリボンは何本とれそうですか。
5本だと思います。
5.5本かもしれないです。
5.5本っておかしくないですか。
なるほど。「何本ですか」と聞かれているので、5.5本などではなく、5本や6本という整数の答えになるとよさそうですね。では、まず問題を解いてみましょう。
※各自、ノートに計算をする。商を小数まで割り進めている子供には個別に支援をする。
では、答えから確認します。答えはいくつになったでしょうか。
5本です。
他の答えの人はいませんか。
私も5本です。6本だと3×6=18で16.4mを超えてしまいます。
答えは5本でよさそうですね。では、余りはいくつになりましたか。
14mです。
1.4mです。
余りは14mじゃないんですか。
えっ。余りは1.4mだと思います。
14mと1.4mの2通りの余りが出てきましたが、それぞれどのように考えたのでしょうか。
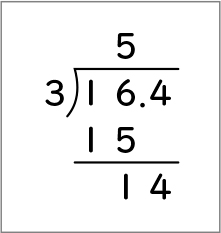
私は余りが14だと思います。筆算で考えると16の中に3が5個入ります。商を5にして3×5=15で、16から15を引くと1になります。1の中に3は入らないので、4を下ろします。だから、余りは14になりました(図1)。
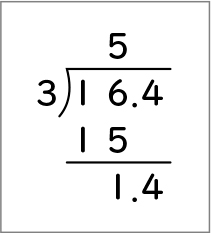
僕は余りが1.4だと思います(図2)。余りが14だと、まだ3mのリボンが切り取れるからおかしいです。
どういうことですか。
余りが14なら、まだ3で割れます。
うーん。どちらが正しい余りなのだろう。
どちらの余りが正しいのでしょうか。

16.4÷3の余りは、14と1.4のどちらでしょうか?
見通し
割る数と余りの大きさを比べればよさそうだな。
確かめの式を使えばどちらの余りが正しいか分かるかな。
テープ図をかいて、3mずつ切り取っていけば、余りが分かりそう。
自力解決の様子
A つまずいている子
・余りの大きさが14と1.4のどちらか分からず、止まっている。
B 素朴に解いている子
・割る数と余りの関係に着目し、余りが割る数より大きいことに気付いて、余りを1.4と考えている。
C ねらい通り解いている子
・確かめの式とテープ図を結び付けながら、 商と余りの関係を視覚的に捉え、その大小関係を根拠に説明している。
全体発表とそれぞれの考えの関連付け
それでは発表してもらいます。
私は、余りは割る数より小さくなるという関係を使って考えました。もし余りが14だとすると、割る数の3より余りの14のほうが大きくなるので、まだ 3で割ることができます。だから、余りは14ではないことが分かりました。だから余りは1.4だと思います。
なるほど。割る数より余りが大きいから、余りは14ではなさそうですね。
「割る数と余りの大きさの関係を使うと余りが14にはならなそう」という、この考え方には納得できますか。
はい。納得です。でも、余りが14ではないことは分かったけれど、余りが1.4になる理由がまだ分からないです。
そうですね。では、どうして余りが1.4になるのかについて、説明してくれる人はいますか。
はい。僕は余りが14と1.4のどちらかをはっきりさせるために、確かめの式を使って考えました。確かめの式は「割る数×商+余り=割られる数」なので、3×5+余り=16.4になる余りはどちらかを考えました(図3)。

余りが1.4のときは、3×5+1.4=16.4になります。だから、余りは1.4になると思いました。
余りが14のときは、3×5+14=29になってしまって、割られる数が16.4にならなくなってしまうのでおかしいと思います。
なるほど、確かめの式を使うよさは何ですか。
確かめの式を使えば、どちらの余りが正しいのか分かります。
確かめの式を使えば、商だけでなく、余りが正しいかも確かめられますね。他の方法で考えた人はいますか。
僕はテープ図を使って考えました(図4)。
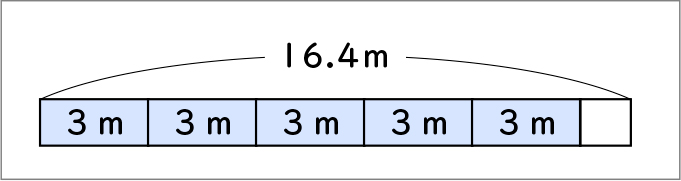
まず、16.4mのテープ図の中に3mずつ区切りを入れていきます。5回の区切りが入ったところで、もう3mのテープが取れないことが分かります。3mが5本なので3×5=15で、15m切り取ったことになります。
テープ図で考えると、余りはどうなりましたか。
16.4mから15m切り取ったから、16.4-15=1.4なので余りは1.4mになります(図5)。
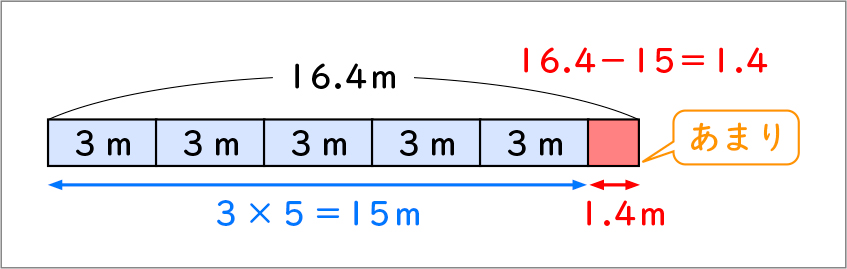
図の中のどこが余りの1.4mですか。
この赤い部分です。
テープ図で表すと、割る数の3mより余りのほうが小さくなると思いました。
あと、テープ図を使うと、確かめの式の意味がよく分かります。
今、確かめの式とテープ図を使って、余りが1.4になることが分かりました。ここで、最初の筆算に戻って考えてみましょう。筆算で考えると、余りの小数点の位置はどのように考えればいいですか。(図6)
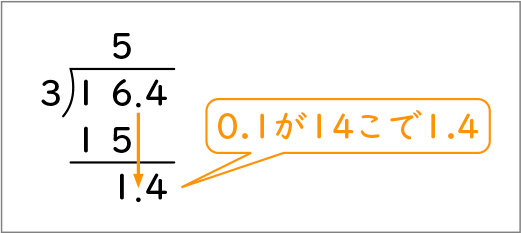
小数のわり算の余りを考えるときは、余りの小数点は割られる数の小数点にそろえて打つとよいと思います。
どうしてですか。
余りが14だと、割る数の3より大きくなってしまうからです。
この14は、0.1が14個あるという意味だから1.4になると思います。
なるほど。みなさんが言ったように、小数のわり算で余りが出る場合は、割られる数の小数点の位置にそろえて、余りの小数点を打てばよさそうですね。
ふり返りとまとめ
今日は、16.4÷3の余りについて考えてきました。余りの大きさに迷ったときは、どうすればよかったですか。
割る数と余りの大きさの関係で考えるとよいです。
確かめの式を使えば、商だけでなく、余りが正しいかも確認できました。
テープ図を使うと、余りの大きさを確かめやすくなります。
そうですね。今まで学習してきたことを使って、余りが正しいかを確認できる方法がたくさんありましたね。最後に、今日の学習をまとめましょう。
まとめ
- 余りが分からないときは、確かめの式やテープ図を使って確かめることができます。
- 小数のわり算の余りを考えるときは、余りの小数点は割られる数の小数点にそろえて打ちます。
評価問題
商は1の位まで求めて、あまりも求めましょう。また、計算のたしかめもしましょう。
①29.8÷6(本時の問題と構造が同じ問題)
②94.6÷8(本時の問題と構造は同じだが、商が2桁になる問題)
③67.4÷12(本時の問題と構造は同じだが、割る数が2桁になる問題)
子供に期待する解答の具体例
①29.8÷6=4 余り5.8
6×4+5.8=29.8
②94.6÷8=11 余り6.6
8×11+6.6=94.6
③67.4÷12=5 余り7.4
12×5+7.4=67.4
感想例
- 余りが14と1.4で迷ったけれど、確かめの式やテープ図を使うと自分で確かめられる。
- 余りは割る数より小さくなるという関係は、小数のわり算のときでも同じだと気付いた。
- 余りの小数点は、割られる数の小数点にそろえて打つことが分かった。
ポイント&アドバイス
構成/桧貝卓哉 イラスト/横井智美 図版作成/永井俊彦

