小3算数「かけ算の筆算2けた」指導アイデア《1位数×何十の計算の仕方》

執筆/埼玉県吉見町立西小学校教諭・吉田典正
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、埼玉県三郷市立立花小学校教頭・神谷直典
目次
年間指導計画
・かけ算
・時刻と時間
・わり算
・たし算とひき算の筆算
・棒グラフと表
・余りのあるわり算
・長さ
・暗算
・かけ算の筆算 1けた
・1万を超える数
・円と球
・重さ
・わり算や分数
・何倍でしょう
・小数
・分数
・三角形と角
・計算の順序
・式と計算
・かけ算の筆算 2けた
・そろばん
単元の展開(各時の主な学習活動内容)
第1時(本時)1位数×何十の計算の仕方
第2時 2位数×何十の計算の仕方
第3時 2位数×2位数の計算の仕方(12×23)
第4時 2位数×2位数(12×23)の筆算の仕方
第5時 2位数×2位数の計算の仕方(58×46)、繰り上がりあり
第6・7時 3位数×2位数の計算の仕方、筆算の仕方
第8時 簡単な場合の2位数×1位数の暗算の仕方
第9時 十進位取り記数法及び筆算の仕組みのよさを感得する。
第10時 学習内容の習熟を図り、活用した見方・考え方をふり返る。
本時のねらい
1位数×2位数の計算の仕方を、これまでのかけ算の学習を基に考えることができる。
評価規準
1位数×2位数の計算の仕方を、これまでのかけ算の学習を基に考えている。
本時の教材のポイント
3年生では、これまでに九九表を下に広げる計算(2位数×1位数、3位数×1位数)や×10の計算を学習してきています。本単元では、これらの既習を活用し、九九表を横に広げる計算(×2位数)の計算の仕方を学習していきます。
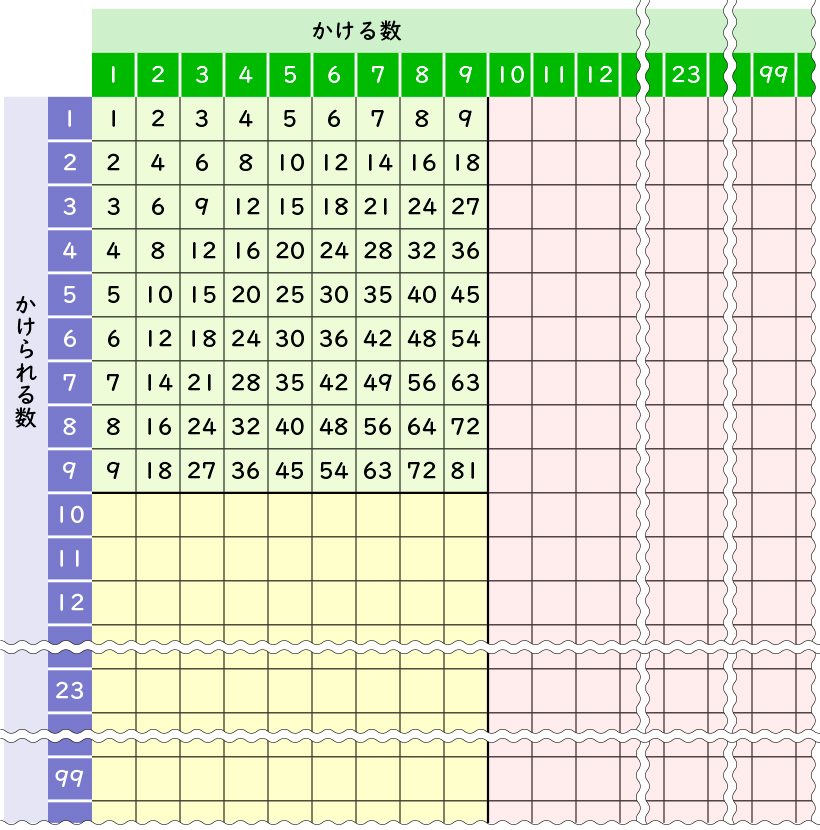
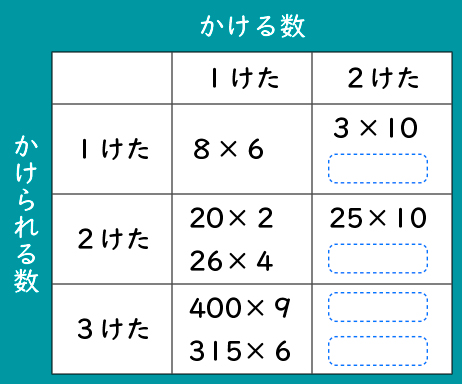
1位数×何十の計算の仕方を考える際には、これまでに習った式に直して計算ができることに気が付かせることが大切です。そのために導入では、今までにどんなかけ算の勉強をしたのかをふり返り、表にまとめる活動を扱っていきます。ここでは既習と未習を明確にすることで、本単元の課題を明らかにし、見通しを持って学習に取り組めるようにしていきます。
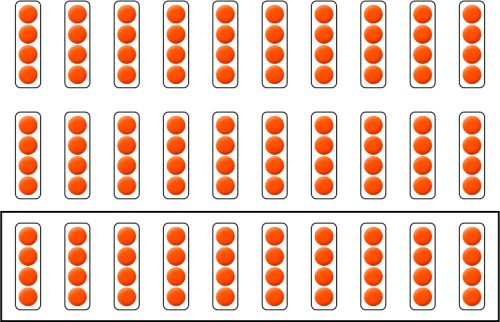
問題場面は4人がけの長椅子が30台あるという設定にします。問題場面から立式をした際に、先程の表から未習であることを確認し、課題を設定します。次に問題場面をアレイ図で下のように表します。この図に着目することで、縦1列に何人座れるのか、それが何列あるのかと問うことで、12×10や40×3といった既習の計算を用いて解決することができるようになります。
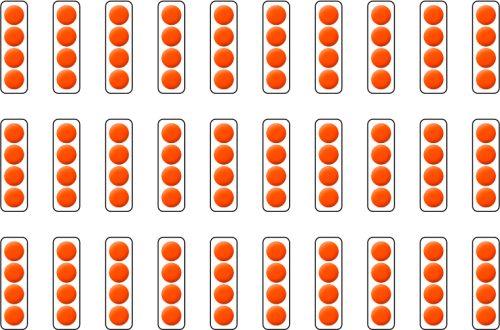
次に、4×30と立式ができた後の計算の仕方について考えます。ここでは、30を3×10と捉えて、×10をつくることが大切です。そのため、子供から出てきた考えを1つの式(4×3×10)に表すことによって、30を3×10と捉えたことに気が付けるようにしていきます。また、手がつかない子供には、縦1列に「何人が座れるのか」や「それが何列あるのか」を問い、図に着目することで×10に気が付けるようにします。また、子供の中には、以前の30×4の計算のように、4×30も4×3の答えに、0を1つつけて120と答えを求めることも考えられます。その際は、安易に認めずに30×4のときと同様に考えてよいかを問うことで、確かめようとする姿勢を育てることも大切にしていきます。この0を付けることが×10と結び付いたり、掛けられる数と同様に掛ける数も10倍になると、答えも10倍になることに気付いたりすることで理解を深めることができます。
本時の展開
これまでにどんなかけ算の勉強をしてきたのかをふり返りましょう。
かけ算九九を習いました。
1桁×1桁はできるようになりましたね。
20×2とか、315×6もできるようになりました。
掛けられる数が大きくなっても計算できるようになりましたね。
掛ける数も3×10や25×10のように、10倍なら計算できます。
そうですね、表にまとめるとできるようになったことが分かりますね。では、今回はこんな問題を考えてみたいと思います。

1台の長いすに4人ずつすわります。30台の長いすには、全部で何人すわれますか。
人数を求める式を立ててみましょう。
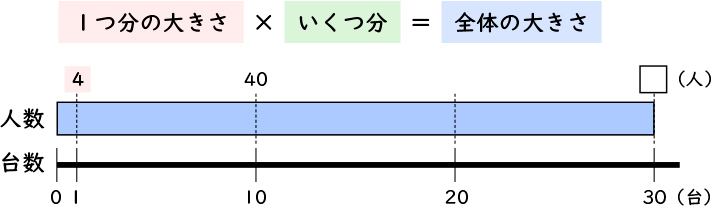
4×30になります。
これまでのかけ算の式との違いは何ですか。
掛ける数が大きくなっています。何十を掛ける計算はまだ学習していません。
どのように計算したらいいのでしょう。
掛ける数が大きくなってもこれまでの学習を使って計算できないかなあ。
どうすれば、いままでに学習した計算が使えますか。

何十を掛ける計算の仕方を考えよう。
見通し
図を基に考えてみよう。
かけ算のきまりを使って計算してみよう。
自力解決の様子
A つまずいている子
・同数累加の考えで答えを求めようとするが、計算が大変になり、答えを求めることができない。
B1 素朴に解いている子
・横一列を1つのまとまりとして考え、それが3列あるので4×10=40。40×3=120と既習の計算を基に考えている。
B2 素朴に解いている子
・既習の40×3と同様に、4×30も、4×3=12 0を1個つけて120。
C ねらい通り解いている子
・縦1列を1つのまとまりとして考え、それが10列あるので 4×3=12。12×10=120と既習の計算を基に考えている。
ノート例

全体発表とそれぞれの考えの関連付け
それでは発表してもらいます。B1さんはどのように計算しましたか。
まず横1列の人数を求めました。横1列の人数は4×10で40人です。40人が3列あるので40×3で120人になります。
1つの式に表すとどんな式になりますか。
(4×10)×3になります。
前に学習した何十×いくつと同じ形になりましたね。これなら計算できます。
次に、B2さんはどのように計算しましたか。
4×3=12。12の10倍だから、0を1個つけて120と計算できます。
以前の学習と同じように、まず4×3=12をしました。そして、12に0を足して120になりました。
40×3のときは、確かにそうやって計算をしましたね。4×30のときも同じように考えていいのかな。Aさんはどうですか。
図を使うと説明できます。まず縦1列の人数を求めました。縦1列の人数は4×3で12人です。12人が10列あるので12×10で120人になります。

1つの式に表すとどんな式になりますか。
(4×3)×10になります。
4×30は、4×3の10倍と見ることができるから、後から0をつければいいのですね。
掛けられる数が10倍になると、答えも10倍になったように、掛ける数が10倍になっても、答えが10倍になるのですね。
2つの考えで同じところや似ているところはどこでしょうか。
どちらもこれまでに習った計算を使って解いています。
掛けられる数も掛ける数も、10倍になると答えも10倍になるところです。
確かにどちらも×10が出てきています。
つまり4×30はどのように直すと今までの計算でできるのですか。
30を3×10のかけ算に直すとできそうです。
計算の仕方を一度まとめてみましょう。

はじめの表を見て、まだ学習していないかけ算はどれですか。
2桁×2桁です。
12×30の計算の仕方をまとめの計算の仕方を使って説明してみましょう。
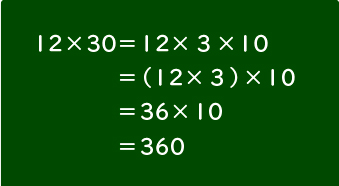
30を3×10に直して計算すればできそうです。
2桁の数×何十の計算でもできそうです。
これからどのようなかけ算をしていきますか。
11×28のような何十ではないかけ算の計算です。
学習のまとめ
- 掛ける数が10倍になると、答えも10倍になる。
- 何十を掛ける計算の仕方は、何十をいくつ×10に直すとこれまでのかけ算の計算でできる。
評価問題
本時ではさらに、2位数×何十の計算に取り組むことにより、本時の学習をふり返ります。
感想例
- 表を見て、「40×3=120」や「4×3=12、12×10=120」のように、これまで習った式に直して計算できることが分かりました。
- 28のように何十ではないかけ算の場合も、これまで習った式に直せば計算できると思う。
- 今度は、何十でない数を掛ける計算を考えたいです。
ポイント&アドバイス
構成/桧貝卓哉 イラスト/横井智美 図版作成/永井俊彦

