小2算数「箱の形」指導アイデア《箱を構成する面の形や面の数を理解する》
執筆/新潟大学附属長岡小学校教諭・荒井琢郎
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、新潟県新潟市立上所小学校教諭・志田倫明
目次
年間指導計画
・表とグラフ
・時刻と時間
・2けたのたし算
・2けたのひき算
・長さ
・1000までの数
・水のかさ
・大きい数のたし算とひき算
・三角形と四角形
・式と計算
・かけ算(1)
・かけ算(2)
・かけ算(3)
・1000より大きい数
・たし算とひき算の関係
・図を使って考えよう
・分けた大きさ
・箱の形
単元の展開(各時の主な学習活動内容)
第1時 身の回りにある箱について、面の形に着目してA(直方体と立方体)とB(それ以外の立体)に仲間分けする。
第2時(本時)牛乳パックの仲間分けについて話し合う活動を通して、箱を構成する面の形や面の数を理解する。
第3時 身の回りにある箱の面を厚紙に写し取り、切ってつなぎ合わせ、箱の形に組み立てる。
第4時 辺の長さや辺や頂点の数に着目して、箱の形を構成する要素について考える。
第5時 練習問題に取り組む。
本時のねらい
箱の形を構成する要素として、面の形は四角形で、6つの面で構成されていることを理解する。
評価規準
「面の形」と「面の数」の2つの視点で、牛乳パックの仲間分けの理由を説明できる。
本時の教材のポイント
前時と本時で、身の回りにある箱の形の仲間分けをする活動を行います。本実践では子供たちが直観的に判断した分類に従い、直方体や立方体を「A:箱の形」、それ以外の立体を「B:特別な形」と呼んで授業を展開します。前時では、子供たちが集めてきた身の回りにある多様な箱(直方体、六角柱、平べったい箱、楕円状のお弁当箱など)を提示し、外観をもとに仲間分けを行いました。この段階で子供たちは「面の形が全て四角形ならばA(箱の形)」「曲面があったり(円柱など)、面が四角形でなかったり(六角柱など)すればB(特別な形)」と捉えています。
本時の導入場面で、子供の認識を揺さぶる教材として牛乳パックを提示します。牛乳パックは、上部が閉じられていると三角形の面が見えるため「B」の仲間のように見えます。しかし、上部を切り開くと面の形が全て四角形で構成されていることが分かり、Aの仲間のようにも見えます。さらに、面の数に着目すると上部が開いていて面が5つしかなくなるため、既習の「箱の形」の条件を満たしません。このように直観だけでは判断に迷う場面をつくることで、本時の学習問題「牛乳パックはAとBのどちらの仲間なのだろうか」を設定します。
本時の展開場面では、牛乳パックの実物を操作したり、前時に扱ったAとBの箱と比較したりしながら、面の形だけでなく、面の数に着目して議論できるように働きかけます。その結果、A(直方体と立方体)は四角形の面が6つで構成されていることを再確認し、牛乳パックは面の数が足りないことから、Bの仲間だという結論を導き出します。
本時の終末場面では、1人1台端末のデジタル教材を活用します。画面上で6枚の四角形を操作し、箱を組み立てるシミュレーションを行うことで、「四角形が6枚揃って初めて箱の形が構成される」ことを改めて確かめます。また、面のつなぎ方によっては箱にならない(重なってしまう)ケースにも触れ、面の配置重要性についても気付きを促します。この経験は、次の時間に学習する、6つの面のつながり方を考える活動で生かされます。
※今回用いたアプリは、下のように面を並べると、どのように箱ができあがるかシミュレーションできるものです。
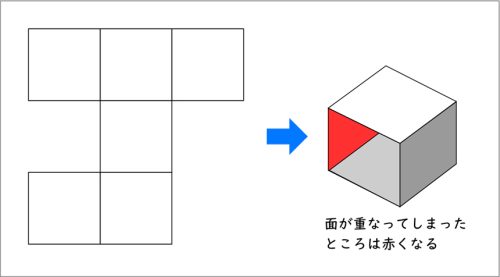
本時の展開
これは「A:箱の形」と「B:特別な形」のどちらの仲間でしょうか。

これは上が斜めになっているからBじゃないかな。
上を切って開けば、「A:箱の形」の仲間になるんじゃないかな。
そうかも!
では、実際に上を切って開いてみますね。
※牛乳パックを切って開く。

やっぱりAの仲間だ!
いや、違うんじゃない? だって、上に穴が開いているよ。
Aだと思う人? Bだと思う人?
(それぞれ子供が挙手をする)
考えが分かれましたね。今日は牛乳パックがAとBのどちらの仲間なのか考えましょう。

牛乳パックはAとBのどちらの仲間なのか考えよう。
牛乳パックのどこに注目すれば、AかBか分かると思いますか。
面の形を見て考えればいいと思います。
上に穴が開いているけど、これでもAの仲間になるのか、それともBの仲間になるのかをはっきりさせたいです。
牛乳パックの面の数を数えてみたらいいと思います。
前の時間に使ったAとBの箱と比べてみたいです。
それでは、牛乳パックの面の形や面の数を調べたり、前の時間に使ったAとBの箱と比べたりしながら、AなのかBなのか決めて、そう考えた理由をノートに書きましょう。
見通し
面の形を調べたらいいと思う。
面の数を調べたらいいと思う。
前の時間に使ったAとBの箱と比べればいいと思う。
自力解決の様子
A つまずいている子
・牛乳パックは面の形を見ると四角形で構成されているからAだと判断しており、面の数に着目できていない。
B 素朴に解いている子
・面はどれも四角形で構成されているが、上が開いている形のため、Aに分類できるか迷っている。
・面の数という視点がないが、上が開いていることを根拠にBだと判断している。
C ねらい通り解いている子
・面の数に着目し、Aの仲間は全て面の数が6つであることから、牛乳パックは面の数が5つであり、Aの仲間に入れることはできないと判断している。
全体発表とそれぞれの考えの関連付け
牛乳パックはAの仲間だと思うみなさんは、Aの仲間だと考える理由を教えてください。
〈C1〉牛乳パックの面の形を調べたのですが、どれも四角形でできているので、Aの仲間だと思います。
面が四角形でできているから、見た目もAの仲間のように見えます。
でも、上に穴が開いているから、違うんじゃないかな。Aの仲間はどれも上が閉まっている形になっているよ。
C1さんは面の形が四角形ということに着目したのですね。しかし、上に穴が開いているから、Aかどうかはっきりしないと言っている人もいますね。
Bの仲間だと考えるC2さんはどう思いますか。
〈C2〉牛乳パックの面の数を数えてみました。前の時間に、Aの仲間は面の数がどれも6つでしたよね。でも牛乳パックは面の数が5つしかありません。だから、Aの仲間とは言えないと思います。
確かに。面の数で考えるとAの仲間には入れないね。
C2さんは面の数に着目したのですね。では、Aの仲間は、どういう仲間だと言えますか。
Aの「箱の形」は、面の形が全部四角形だと思います。
Aの「箱の形」は、全て面の数が6つだと思います。
みんなが考えるAの仲間は、面の形が四角形で、面の数が6つなのですね。そう考えると、牛乳パックはBの仲間になるんですね。
面が5つだと絶対に「箱の形」にはならないのかな。
面の数が5つでも箱になるか確かめたいんですね。それでは、電子黒板を見てください。
※教師の端末から立体をつくるシミュレーションを提示する。
このアプリを使うと確かめることができます。このます目をタップすると、面を置くことができます。面をいくつ置くと、Aの箱の形がつくれるでしょうか。
5つだとつくれないと思います。
6つだとつくれると思います。自分の端末でつくってみたい。
7つでもできるかな。
いろんな数の面を確かめてみたいんですね。それでは、1人1台端末を用意して、面を6つつなげて、Aの箱の形をつくってみましょう。
やっぱり面が6つじゃないと箱の形にならないな。
面が6つでも、面の置き方がよくないと箱の形にならないよ。
自分でも面を切って、箱の形をつくってみたいな。
面が6つであることも大切ですが、面の置き方も大切なのですね。次の時間は、厚紙から6つの面を切ってつなげて、実際に箱をつくってみましょう。
まとめ
構成/桧貝卓哉 イラスト/横井智美・やひろきよみ 図版作成/永井俊彦

