小6算数「文字を使った式」指導アイデア《乗法の場面を文字式で表し、文字に当てはまる数の求め方を考える》

執筆/富山県高岡市立木津小学校教諭・屋鋪善祐
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、富山大学附属小学校教諭・羽柴直子
目次
年間指導計画
・対称な図形
・文字を使った式
・場合の数
・分数×÷整数
・円の面積
・分数×分数
・分数÷分数
・角柱と円柱の体積
・資料の調べ方
・小数と分数の計算
・比と比の利用
・拡大図・縮図
・比例と反比例
・およその面積と体積
・算数のまとめ
単元の展開(各時の主な学習活動内容)
第1時 xやyなどの文字を使った式の表し方を知る。
第2時 文字に数を代入して、式の値を求める。
第3時(本時)乗法の場面を文字式で表し、文字に当てはまる数の求め方を考える。
第4時 加法の場面を文字式で表し、文字に当てはまる数の求め方を考える。
第5時 乗法や加法の混じった場面を文字式で表し、文字に当てはまる数の求め方を考える。
第6時 場面や図と式を結び付けて、式を読み取る。
第7時 文字式に様々な数を当てはめ、図形と式を結び付けて、式が表す意味を考える。
第8時 既習事項の確かめをする。
本時のねらい
数量関係に着目し、乗法の場面を文字式で表し、条件に当てはまる数の求め方を考える。
評価規準
場面の数量関係を文字を使った式で表し、条件に当てはまるxの値を、簡潔に求めることができる。
本時の教材のポイント
本時では、数を入れると、他の数に変わる箱を教材にします。数を入れる前後の2つの数量の関係を文字x、yを用いた式で表していきます。まずは全体で、箱に入れた数が何に変わるか予想したり、結果を確認したりする場を設けます。モニター画面に1、2回例示すると、「4倍した数に変わる」という規則性に気付く子供が出てくるでしょう。その瞬間の子供の反応を捉え、「どうして分かったの?」「なぜ『やっぱり』と思ったの?」など問い返すことで、数量の関係性を全体に広めることができます。
また、「他の数でもできる!」など発展的に考え、主体的に活動しようとする子供の姿も生まれるでしょう。その際、数量関係をxやyを用いて式に表した既習内容を想起させ、場面を文字を使った式に表し、条件に当てはまる数を求める展開につなげていくことで、本時のねらいに向かって子供自ら歩み出すことができます。
問題解決に困難を感じる子供がいる場合は、別の数でも試してみると、数量関係の規則性に気付きやすくなります。見通しの場面では、「〇(最初の数)を4倍したら、△(後の数)になる」ことをていねいに確認し、場面を図に表し、板書に位置付けましょう。図・式・言葉を関連付けることで、見通しをもちながら一人一人が考えをもつことができます。
本時の展開

箱に数を入れると、どんな数に変わるでしょうか?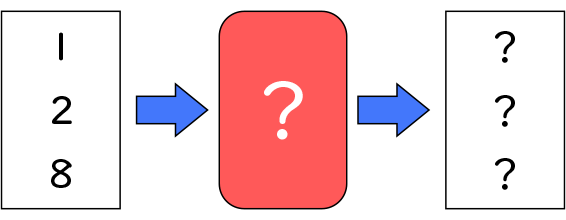
ここに箱があります。この箱は、数を入れると、別の数に変わる箱です。さあ、どんな数に変わるでしょう。
楽しみだな。
1を入れます。どんな数に変わるでしょう?
2! 4! 10!
実は、1を入れると……、「4」になります。(ICTで提示)
本当だ、1が4に変わった!
では、次は2を入れてみましょう。どんな数に変わるでしょう。
5です!
いや、8ではないですか?
実は、2を入れると……、「8」になります。(ICTで提示)
当たった! やっぱり!
なぜ、やっぱり「8」になると思ったのですか。
あるきまりに気付いたから、8になると思いました。
何かきまりがあるのですか。
はい!
きまりに気付いたのであれば、他の数でも予想できそうですか。例えば、「8」でもできますか。
できそうです! どんな数でもできると思います。
「どんな数でも」と発言がありましたが、これまでいろいろと変わる数を文字で表すことを学習していましたね。どんな文字でしたか。
xやyです。
これまで習ったxとyを使って、このきまりを式に表せそうです。
では、xとyを使った式に表し、変わった後の数を求めてみましょう。

xとyを使った式で表し、変わった後の数の求め方を考えよう。
見通し
もっといろいろな数を試して、きまりを見付けよう。
いろいろな数をxに入れて、変わった後の数を見付けよう。
x×4=y(前の数の4倍が、変わった後の数)のきまりを使って考えよう。
自力解決の様子
A つまずいている子
・4倍になっていることに気付かず、xとyを使った式に表すことができない。
B 素朴に解いている子
・乗法の場面を文字式に表して、小さい数から順番に、xに数を当てはめて導き出すことができている。
x×4=y
1×4=4
2×4=8

8×4=32
C ねらい通り解いている子
・乗法の場面を文字式に表して、式の意味を理解している。また、簡潔にxに数を当てはめて導き出すことができている。
x×4=y
変わる前の数×4=変わった後の数
8×4=32
ノート例
B 素朴に解いている子

A つまずいている子

全体発表とそれぞれの考えの関係付け
構成/桧貝卓哉 イラスト/横井智美 図版作成/永井俊彦

