小６算数「場合の数」指導アイデア《表や図を用いて、順列について、落ちや重なりなく調べる方法を考える》

旅行に行きます。おばあちゃんの家に行って雪遊びをします。

最初に雪合戦をしたいです。次に雪だるまをつくって、次にそり遊びをして、最後にかまくらづくりをしたいです。

私は、そり遊びからしたいです。そりで遊んで、雪合戦をしてから、かまくらをつくり、最後に雪だるまをつくろう。

僕も、まずはそり遊びがいいです。でも、次は雪合戦ではなくて、かまくらをつくりたいです。

すでに３通りも出てきたから、遊ぶ順序はたくさんありそうです。

全て書き出してみたら分かりそうです。

確かに！　遊ぶ順序を全て書き出してみよう。

全て書くのは、すごく大変です。

言葉が長くて書くのが大変です。

短くしたらどうですか。雪合戦は「ゆ」、そり遊びは「そ」。

いい考えだと思います。でも、それでは雪合戦も雪だるまづくりも「ゆ」になってしまいます。

賛成です。

記号で表すと書き出しやすかったです。全て書き出せました。

私も全て書き出せました。全部で20通りありました。

えっ!?　僕は18通りになりました。

私は26通りです。

僕は15通りです。26通りと15通りでは、11通りも違います。

２人のノートを見せてください。

○○さんのノートには、ウ－ア－イ－エの順序がないです。

私も、その順序を書き忘れていました。

あれ？　よく見たら、同じ順序を２つ書いていました。

正確に全て書き出すことはできないのかもしれません。

今は、思いつくままに書き出していました。順番に書き出してみたらどうでしょうか。

まずは雪合戦を１番にして、その後の遊びの順序を考えます。

雪合戦を１番にして、その後の順序を考えてみよう。

表に整理してみよう。

図に表してみよう。

６通りです。

あれ、僕は７通りになったよ。

どうやって考えたのですか。

雪合戦を１番にすることから、「ア→」から描き始めて、その後に続くイ、ウ、エの順序を思い付くだけ書き出してみました。

あれ、ア→ウ→イ→エが２つあります。

本当だ。それを消すと６通りになるね。

雪合戦（ア）を最初にすることに決めても、その後の順序を思い付いた順番で書き出すと、落ちや重なりが出てきそうです。どうしたらいいのだろう。

私は表にかいて整理したよ。表で表すと落ちや重なりが分かりやすくなって、最後に確かめると重なりがあったから消しました。

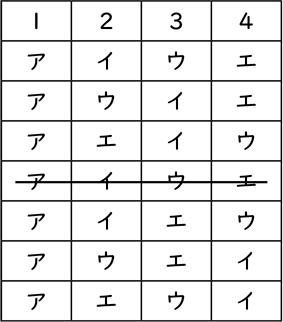
なるほど。落ちや重なりがないか確かめればよいのだね。

でも、表で表しても結局落ちや重なりが出てくるのか。

Ａさん　順番に書き出すことだと思います。

Ａさん　最初に雪合戦（ア）をすることを決めたら、２番目に遊ぶ遊びは、そり遊び（イ）か、かまくらづくり（ウ）か、雪だるまづくり（エ）のどれかになります。例えば、２番目にそり遊び（イ）をすると決めます（図①）。すると、３番目は、かまくらづくり（ウ）か、雪だるまづくり（エ）になります（図②）。３番目が決まれば、残ったほうが４番目になります（図③）。

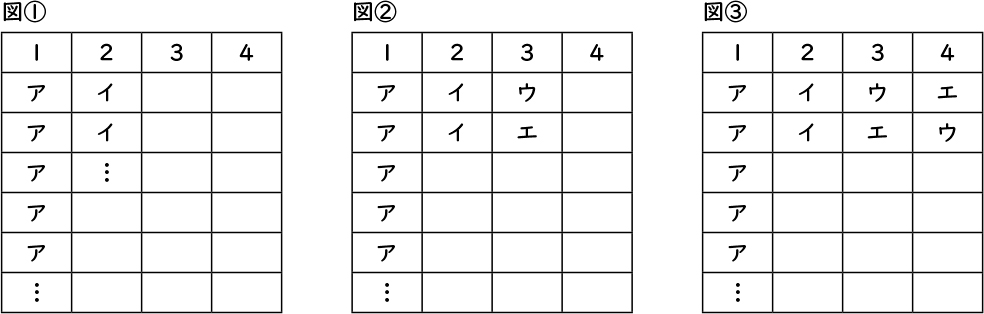
なるほど。２番目にそり遊び（イ）が来る順序は、２通りだということが分かります。

次は、２番目にかまくらづくり（ウ）をする場合を同じように書いたらいいですね（図④）。

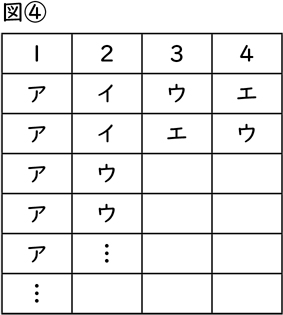
Ａさん　２番目にかまくらづくり（ウ）が来る順序も２通りです。

最後は、２番目に雪だるまづくり（エ）をする場合を同じように書いたらいいね。

Ａさん　最初に雪合戦（ア）をする順序は６通りです（図⑤）。

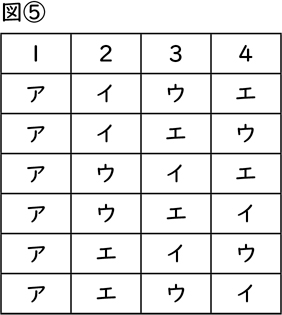
Ａさん　この方法だと、落ちや重なりなく調べられます。

最初にそり遊び（イ）やかまくらづくり（ウ）、雪だるまづくり（エ）をする場合も、この方法で調べてみたいです。

できました。最初にそり遊び（イ）をする場合も、かまくらづくり（ウ）をする場合も、雪だるまづくり（エ）をする場合も、それぞれ６通りありました。

私も同じ結果になりました。だから、雪遊びをする順序は24通りです。

Ｂさん　僕も同じように考えましたが、表ではなく図にしました。

Ｂさん　ピンクで囲んだところが１番目の遊びです。この図は、雪合戦のアです。３つに枝分かれした黄緑で囲んだところが２番目にする遊びです。

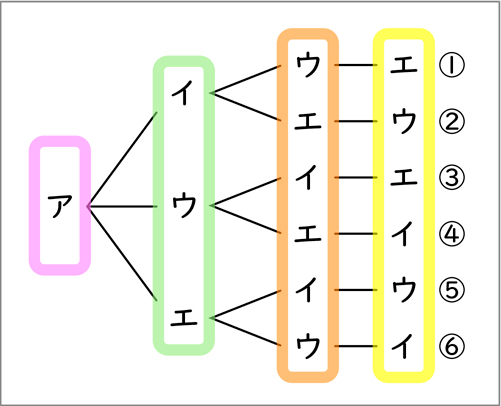
そういうことか！　１番目はアだから、２番目はイかウかエになるということですね。

ということは、オレンジで囲んだところは、３番目にする遊びを表しているのですか。

Ｂさん　そうです。「ア－イ」と来たら、３番目はウかエが来ることを表しています。

さっきの表とは、表し方は違うけれど、同じように考えているのですね。

黄色で囲んだところは、４番目にする遊びを表しているのですね。

Ｂさん　だから、①ア－イ－ウ－エ、②ア－イ－エ－ウ、③ア－ウ－イ－エ、④ア－ウ－エ－イ、⑤ア－エ－イ－ウ、⑥ア－エ－ウ－イの６通りということが分かります。

はい。表と同じ考え方でした。

Ｂさん　枝分かれするように書くので、同じ記号を何度も書かないところは表と図の違いです。

図に表して考えるのも、順序よく調べられて便利です。

イやウやエが１番のときの図も書いて調べてみたいです。

できました。やっぱりそれぞれ６通りありました。だから、雪遊びする順序は、全部で24通りです。

はい。いいです。

Ｃさん　僕、気が付いたことがあるんですけど……。表や図を全部書く必要はないと思います。

Ｃさん　１番にアがくるときを表や図で調べたら、あとは計算で求めることができます。

そういうことか！　イ、ウ、エが１番にくるときも、アと同じ６通りあるから、６×４で24通りと求められるのですね。

確かに！　この方法だったら遊びの種類が５つ、６つ……に増えても、１つだけ表や図で調べたら、あとはかけ算で求めることができます。

Ｂさんの図で考える方法が、私はやりやすいです。

表で考える方法は、結果が見やすいからいいです。

表や図で１つ目のアを調べた後は、計算で全部の順序が何通りになるかを求めるといいです。