小2算数「かけ算(2)」指導アイデア《9の段の九九の構成を通して、答えの増え方や交換法則に気付く》
執筆/新潟県新潟市立両川小学校教諭・長沢圭祐
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、新潟県新潟市立上所小学校教諭・志田倫明
目次
年間指導計画
・表とグラフ
・時刻と時間
・2けたのたし算
・2けたのひき算
・長さ
・1000までの数
・水のかさ
・大きい数のたし算とひき算
・三角形と四角形
・式と計算
・かけ算(1)
・かけ算(2)
・かけ算(3)
・1000より大きい数
・たし算とひき算の関係
・図を使って考えよう
・分けた大きさ
・箱の形
単元の展開(各時の主な学習活動内容)
第1時 6の段の九九を構成する。乗数が1増えると、積は被乗数分だけ増えることを理解する。
第2時 6の段の九九の呼称を知り、唱える。6の段の九九を用いて、問題を解決する。
第3時 7の段の九九を構成する。乗数が1増えると、積は被乗数分だけ増えることを理解する。
第4時 7の段の九九の呼称を知り、唱える。7の段の九九を用いて、問題を解決する。乗数の交換法則が成り立つことに気付く。
第5時 8の段の九九を構成する。8の段の九九の構成を通して、答えの増え方や交換法則に気付く。
第6時 8の段の九九の呼称を知り、唱える。8の段の九九を用いて、問題を解決する。
第7時(本時)9の段の九九を構成する。9の段の九九の構成を通して、答えの増え方や交換法則に気付く。
第8時 9の段の九九の呼称を知り、唱える。9の段の九九を用いて、問題を解決する。
第9時 1の段の九九を構成する。1の段の九九の呼称を知り、唱える。1の段の九九を用いて、問題を解決する。
第10時 問題文の仕組みを読み取って加法や減法・乗法の演算決定をし、乗法の理解を深める。具体物の操作を基に、解き方や絵や図、式や数字、言葉を使って分かりやすく説明する。
第11時 学習内容の定着を確認するとともに、数学的な見方・考え方についてふり返る。
本時のねらい
9の段の九九について、アレイ図や式を使って考える活動を通して、既習のかけ算や計算に関して成り立つ性質を用いて構成の仕方を説明することができる。
評価規準
9の段の九九について、既習のかけ算や計算に関して成り立つ性質を用いて、図・式・言葉などの多様な表現方法で構成の仕方を説明することができる。
本時の教材のポイント
これまでに子供は、2~8までの段の九九を学び、乗数が1増えると積が被乗数分だけ増えるきまり(乗数と積の関係のきまり)や、分配法則と交換法則などを理解してきています。本時では、これらの既習を活用することで、子供自身が9の段を構成することをねらいとします。教材のポイントは次の3点です。
1点目は、「アレイ図の使用」です。本単元においては、九九を構成する際にアレイ図を用います。アレイ(array)は「配列」という意味であり、その配列の見方は多様です。そのため、子供が多様な考えを基に九九を構成する際に有効です。また、1人1台端末を用いてアレイ図に線を引いてまとまりをつくったり、数字や式を書き込んだりすることで、子供は試行錯誤しながら九九の構成について思考することができます。
2点目は、「図と式と言葉の関連付け」です。九九の構成では、図、式、言葉を関連付けながら説明する活動を重視します。図、式、言葉がそれぞれ独立した状態ではなく、「この図からどんな式が見えるでしょうか」「この式はどんな図に表せるでしょうか」「○○さんが言ったことは、どんな図や式に表せるでしょうか」と問いかけながら、言葉による図と式の関連付けを促します。この活動により、説明する力を養うとともに、子供の理解を深めます。
3点目は、「既習の活用」です。かけ算はたし算を基盤とした、同数累加として意味付けられています。九九の単元では、既習の段の九九や「乗数と積の関係のきまり」「交換法則」「分配法則」などを活用し、新たな段の九九を構成していきます。本単元を通して既習を活用できるように、既習の九九については教室に掲示していきました。また、既習の計算に関して成り立つ性質について、子供たちからアイデアが提案された際、「乗数と積の関係のきまり」を「増える作戦」、「交換法則」を「反対作戦」、「分配法則」を「さくらんぼ作戦」と、子供たちの言葉を基にラベリングし、解決に活用できるようにしました。
本時では「本当に今までのかけ算の考え方を使えるのか」という問いを中心に据えます。課題把握では、9×9の計算は同数累加では大変であり、「8の段までのかけ算」や「交換法則」が使えないという、既習の考え方の限界に着目させます。練り上げにおいては、9×9の解決過程をふり返り、「今までの考え方を使えたのか」という問いを基に、既習の段の九九や既習の計算に関して成り立つ性質を活用していたことを価値付けます。
この3点を意識した授業を本単元を通して繰り返し行うことで、子供は既習を生かして九九を構成しようとするようになります。こうした姿勢は、算数を自ら創り出していこうとする態度の育成につながります。
本時の展開
今度、何チームかで野球の大会があります。試合に出る選手は全部で何人になるでしょうか。
野球は9人でやるから、チームの数が分かれば数えられます。
2チームなら選手は何人ですか。
9+9=18で18人です。
9×2=18のかけ算でもできます。
3チームなら選手は何人ですか。
9+9+9=27だから、9×3=27で27人です。
今までの「はんたい作戦」を使えば、3×9=27のように、ひっくり返して簡単に計算できます。
「はんたい作戦」を使えば、何チームでも分かりそうだね。
いいアイデアですね。今までに学習した考えを使って、9の段をつくろうとしていますね。
4チームなら、9×4=4×9=36で36人。5チームなら、9×5=5×9=45で45人。6チームなら、9×6=6×9=54で54人。
7チームなら、9×7=7×9=63で63人。8チームなら、9×8=8×9=72で72人。9チームなら、9×9=9×9⋯⋯あれ? 「はんたい作戦」を使っても9×9のままだ。
今までのかけ算の考え方は使えないのかな。
数も大きいね。9×9はどうやって考えればいいのかな。

今までの考えを使って、9×9を考えることはできるかな。
見通し
9×9は、だいたいどのくらいだと思いますか。
100くらいかな。
10×10が100だから、100よりは小さい。
考えるときに、何が使えそうですか。
アレイ図で考えよう。
式で考えよう。
今までのどんな作戦が使えそうですか。隣の人に聞いてみましょう。
どんな作戦が使えそう?
反対作戦(交換法則)で9×8=8×9にして、増える作戦(乗数と積の関係のきまり)で9を足そうかな。
さくらんぼ作戦(分配法則)で、9×9を5の段と4の段に分けようかな。
さくらんぼ作戦(分配法則)で、9×9を9×5と9×4に分けようかな。
アレイ図で、9×9の考え方を説明しましょう。何を使って考えるのか、どんな作戦で考えるのか、自分で決めて考えましょう。1つできた人は、いろいろな方法で説明を考えましょう。
自力解決の様子
A つまずいている子
①【数え上げ】
●を1つずつ数えている。
②【同数累加による数え上げ】
9個の●を1まとまりで囲み、9の9個分を数えている。
③【分配法則の適用方法が不明】
9を分けているが、9×9の積が求められない。
B 素朴に解いている子
①【交換法則】【乗数と積の関係のきまり】
8個の●を1まとまりで囲み、8の9個分と9を合わせた図を描いている。
②【被乗数分配法則】
9個の●を2つに分けて囲み、5の9個分と4の9個分などに分割した図を描いている。
③【乗数分配法則】
9個の●を1まとまりで囲み、9の5個分と、9の4個分などに分割した図を描いている。
C ねらい通り解いている子
①【交換法則】【乗数と積の関係のきまり】
8個の●を1まとまりで囲み、8の9個分と9を合わせた図を描き、立式している。
②【被乗数分配法則】
9個の●を2つに分けて囲み、5の9個分と4の9個分などに分割した図を描き、立式している。
③【乗数分配法則】
9個の●を1まとまりで囲み、9の5個分と9の4個分などに分割した図を描き、立式している。
全体発表とそれぞれの考えの関連付け
アレイ図を使って、9×9をどのように考えましたか。
【交換法則】【乗数と積の関係のきまり】(反対作戦+増える作戦)
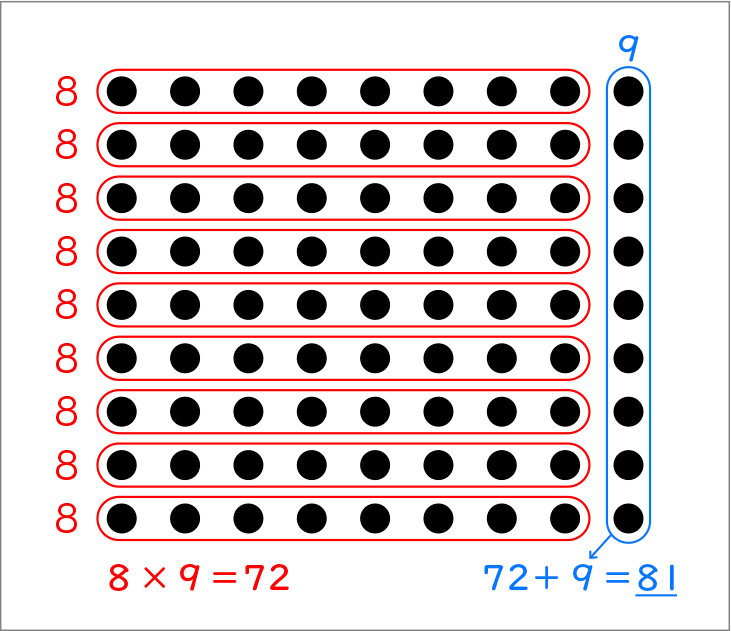
反対作戦で9×8を8×9=72と考えました。9ずつ増える作戦を使うと、72+9=81なので、9×9=81になります。
さくらんぼ作戦も使えそうです。
アレイ図をどのように見ると、さくらんぼ作戦を使って9×9を求められますか。
【被乗数分配法則】(前さくらんぼ作戦)
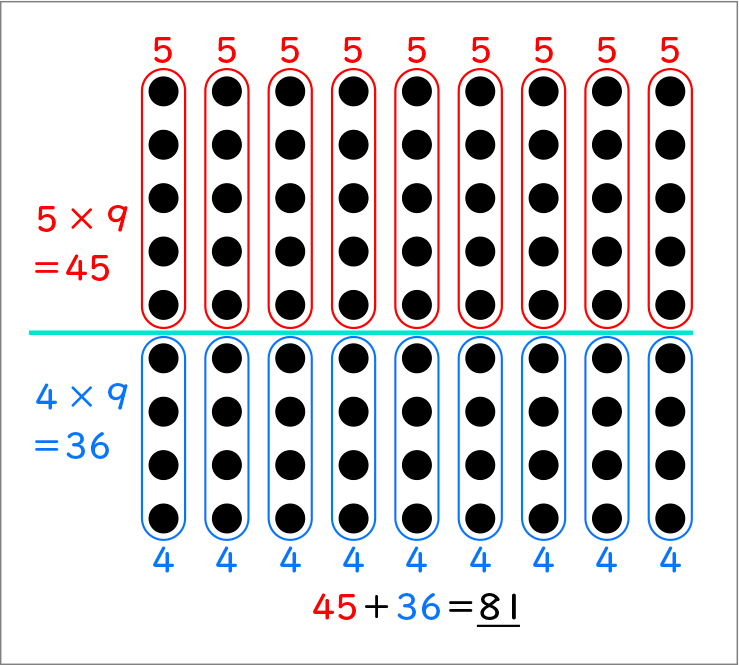
縦の9を5と4で分けます。
9×9を5×9=45と4×9=36に分けて考えました。45+36=81なので、9×9=81になります。
前さくらんぼ作戦で9×9を求められたね。
後ろさくらんぼ作戦でも、9×9を求められますか。
【被乗数分配法則】(後ろさくらんぼ作戦)
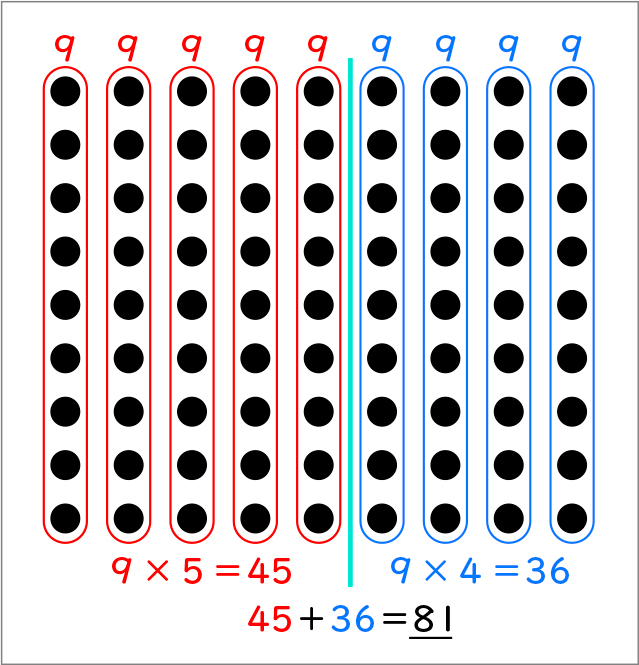
9×5=45と9×4=36にできるよ。
45+36=81になるね。
アレイ図の中に、9×5と9×4は見えますか。
どこだろう。
見えた! 9の5個分と9の4個分で分ける。
いろいろな方法で9×9=81を説明できましたね。最初は、今までのかけ算の考えは使えないのかなと困っていましたね。9×9を解決するために、今までのかけ算の考え方は使えましたか?
(既習を活用して解決した子供の発言について、言及している板書部分を青チョークで示しまとめにつなげる)
今まで学習した段の九九が使えました。
増える作戦で前の九九に9ずつ足しました。
9×8の反対作戦で、8×9を使いました。
9×9を9×5と9×4に分けて考えました。
9×9を5×9と4×9に分けて考えました。
かけ算のきまりや今までの九九が使えました。
まとめ
構成/桧貝卓哉 イラスト/横井智美 図版作成/永井俊彦

