小１算数「３つの数の計算」指導アイデア《３つの数の減法の式の意味を理解と計算》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

授業改善

2025.01.11

プリント

単元の展開

第１時　３つの数の加法の式の意味を理解し、その計算ができる。
▼
第２時（本時）３つの数の減法の式の意味を理解し、その計算ができる。
▼
第３時　３つの数の加減混合の式の表し方や計算の仕方を、操作や図を用いて考え、説明する。

本時のねらい

３つの数の減法の計算で解決できる問題場面について、数量の関係に着目し、計算の仕方を具体物を用いた活動を通して考え、１つの式に表し、計算することができる。

評価規準

３つの数の減法についての問題を、１つの式に表し、解決することができる。（知識・技能）

本時の展開

この前の学習では、３つの数のたし算ついて学びましたね。今日も、紙芝居を用意しました。

※学習者用端末に提示する。

バスに　９人　のっていました。
さいしょの　バスていで　３人　おりました。
つぎの　バスていで　２人　おりました。
バスに　なん人　のこっていますか。

この前との違いを考えながら、お話をききましょう。１枚目。バスに９人乗っていました。２枚目。最初のバス停で３人降りました。３枚目。次のバス停で２人降りました。バスに何人残っていますか。この前のたし算の学習と同じところや違うところは何ですか。

３つの数があります。

人数が減っているところが違います。

ひき算を使うところが違います。

この前のように式をつくって調べられそうですか。

できそうです。

では、今日は、どんなめあてで学習をしますか。

ひき算の式をつくって調べよう。

３つの数のひき算の式に表そう。

３つの数のひき算の仕方を調べよう。

では、めあてを書きましょう。

３つの数のひき算の仕方を調べよう。

見通し

どんな方法で調べるとよいですか。前回のたし算をふり返って考えましょう。

ブロックを並べて考えます。

お話の順番通りに式にします。

では、お話の通りにブロックを動かして、式や答えを考えましょう。式や答えをかいたら、写真に撮って先生に送りましょう。

自力解決の様子

Ａ　つまずいている子

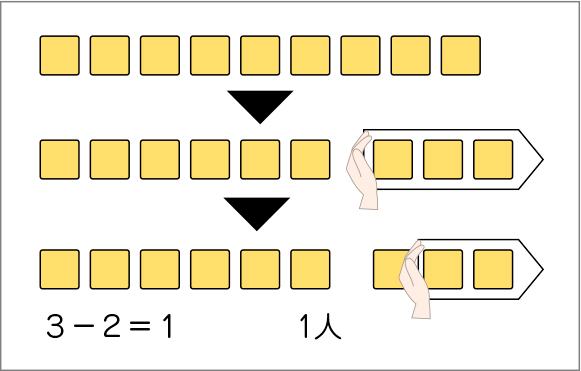
●９個のブロックから６個を動かし、ブロックのまとまりが６個と３個に分かれた後、３個から２個を取り除いてしまう。

Ｂ　素朴に解いている子

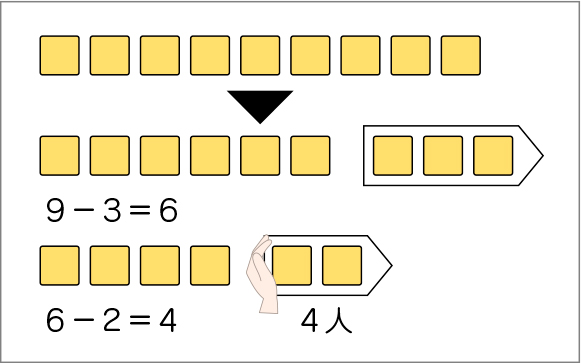
○ブロックの操作を１つずつ、式に表すことができている。
●２つの式を１つの式で表すことはできていない。

Ｃ　ねらい通り解いている子

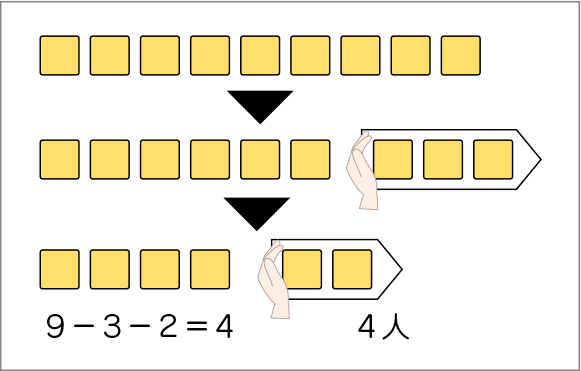
○３つの数の求残の関係を１つの式に表すことができている。
○ブロックの操作と式を関係付けて、左から順に計算することができている。

学び合いの計画

自力解決の段階で、１人１台端末を活用して、前時までの板書を提示しておき、既習内容をいつでもふり返ることができるようにしておきます。また、子供たちが端末の扱いに慣れている場合は、友達の解決方法を共有できるようにしてもよいでしょう。

板書をふり返る方法
・授業後に、教師が板書の写真を撮り、子供に配付する。このときに、時系列で並べておくように指示をする。
自他の解決方法を共有する方法
・自分の考えや操作したものを写真に撮り、データで提出させる。

既習の板書をふり返ったり、事前に互いのつくった式を見合ったりすることによって、ＡやＢの子供は既習のたし算の学習や他者の考えを基に３つの数のひき算の式の表し方や計算の仕方に気付きやすくなります。Ｃの子供は、友達の考えと比較し、自分の考えを見つめる機会になります。

なお、Ａの子供に対しては、やりとりをしながら、９人から６人降りた場面のブロック操作をもう一度させてから、｢どちらのブロックのまとまりがバスに残っている人を表しているかな」などと問うとよいでしょう。このことは、後の全体の交流でもていねいに扱います。

全体の交流では、まず、自分の考えをペアで確認させます。場面を説明しながらブロックを動かすのは大変なので、場面の説明→ブロック操作→場面の説明→ブロック操作という順序で、ゆっくり説明し合うよう促します。

次に、クラス全体で、問題の場面とブロック操作を関連付けていきます。その際、ＡやＢの考えに寄り添います。

Ａの考えは、９個のブロックから３個取り去るところまではできています。最初の操作の結果を絵で確認し、３個のまとまりは降りた人の数、６個のまとまりがバスに乗っている人の数であることを押さえ、２個のブロックを６個のまとまりから取り去ることを理解させます。

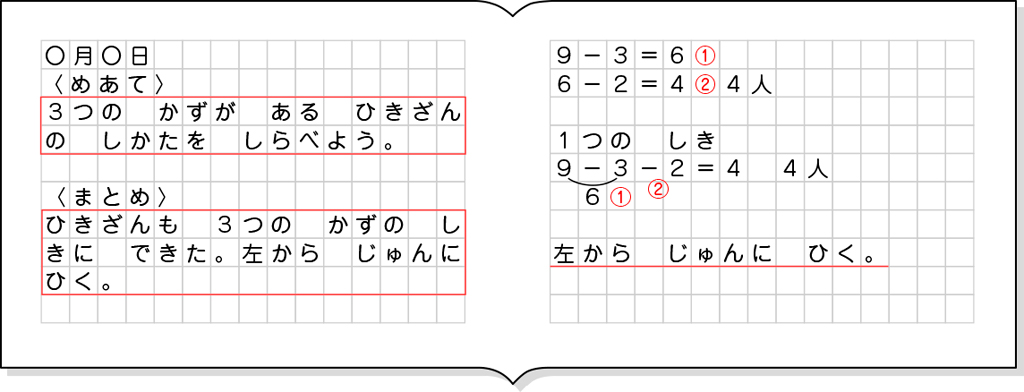
その後、これらの２回のブロックの操作を２つの式で表すというＢの考えを確認します。最後に、前時の学習をふり返りながら、「たし算のときと同じように１つの式で表すことができないかな」と投げかけ、場面を１つの式で表すことを考えていきます。

ノート例

Ａ　つまずいている子

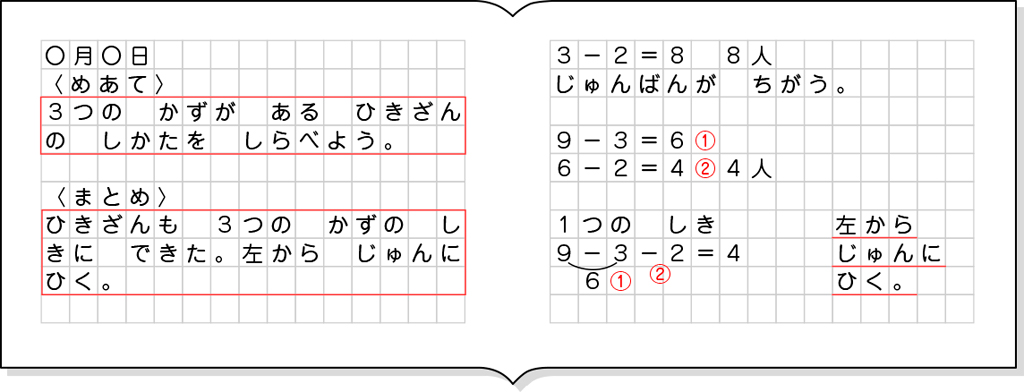
Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

■場面をブロックで操作して表すことの検討

はじめに、ブロックを使ってペアでお話をしてみましょう。

※それぞれの考えを説明させる。

みなさんの様子を見ていると、２つの動かし方があるようです。みんなで確認していきましょう。最初の文章（｢バスに９人……」を指示棒などで指す）をみんなで読みましょう。

※みんなで読む。

この文章は紙芝居ではどの絵のことですか。

１枚目です。

※みんなで読む。

ここまでのお話を、前でブロックで動かして説明してくれる人はいますか。

はじめに９人乗っているから、ブロックを９個並べます（ブロックを並べる）。次に３人降りるから、３個動かします（９個のブロックから３個を引き離す）。

みなさんももう一度、ここまでの動かし方をしてみましょう。

※９個のまとまりから３個を引き離し、６個と３個のブロックが置かれていることを隣同士で確認させる。

みなさんの机の上にブロックが６個と３個になっていますね。バスから降りた人はどちらですか。バスに乗っている人はどちらですか。　

３個は降りた人です。

６個は乗っている人です。

ここまでは、多くの人が同じ動かし方のようでした。では、３つ目の文章（｢つぎの……｣）を読みましょう。

※３つ目の文章を読む。

次にブロックを何個動かしますか。

２個です。

そうですね。今、みなさんの机の上にブロックが６個と３個に分かれています。最初にみなさんに考えてもらったときには、６個から動かした人と、３個から動かした人がいました。どちらかがよいか、隣同士で相談しましょう。

※相談する。

相談の結果を教えてください。前に来て説明できますか。

（６個のブロックを指しながら）バスに乗っているのは６人です。だから、６個のブロックから２個取ればいいと思います。

なるほど。バスに残っているは６人だから、６個のほうから２個取らないといけませんね。ブロックは４個なので、最後に残っているのは４人ですね。

■ブロックの操作から式に表すことの検討

では、今度はブロックの動かし方を式で書いてみましょう。最初の動かし方から順に言ってもらいましょう。

９個から３個取っているから、９－３＝６の式ができます。

次に、６個から２個取っているから。６－２＝４の式ができます。

そうですね。計算しても最後は４人になりましたね。今、式が２つありますが、前のたし算の勉強でしたように、１つの式でかくことができますか。

９－３－２＝４です。

この９－３－２の式では、さっきの９－３と６－２はどこですか。たし算のときのように、①と②の番号を書きましょう。

ところで、最初に考えたときに、９－３－２＝８とした人もいました。このように考えたお友達の気持ちは分かりますか。

３－２を先にしているからだと思います。３－２＝１で、次に９－１をすると８になります。

なるほど。そう言われれば先生も分かりました。このやり方もお話に合っていますか。

最初に乗っていたのは９人で、３人降りたから、最初は３－２ではなく９－３をしないといけません。

そうですね。お話の順に左から順に計算しないといけないようですね。今まで分かったことを基にして、次の問題をやってみよう。（学習者用端末に類似問題を送ったり、別途のワークシートを配付したりする）

バスに　10人　のっていました。　
さいしょの　バスていで　３人　おりました。
つぎの　バスていで　５人　おりました。
なん人　のこっていますか。

ブロックでは、はじめに10個用意します。まず、３個取って７個になります。次に、７個から５個取ります。すると、残りは２個です。１つの式にすると10－３－５＝２。答えは２人です。

学習のまとめ

※「全体発表とそれぞれの考えの関連付け」のやりとりのポイントを黒板に残し、それを使いまとめをする。

今日のめあては、｢３つの数のひき算の仕方を調べよう」でした。どんな式ができて、どんなきまりがありましたか。

ひき算の場面も３つの数の式にできる。左から順にひく。　

評価問題

みかんが　８こ　ありました。
ひるに　５こ　たべました。
よるに　２こ　たべました。
なんこ　のこっていますか。
１つの　しきで　かきましょう。また、けいさんの　じゅんじょを　①、②で　かきましょう。

子供に期待する解答の具体例

８　－　５　－　２　＝　１　　　１個
　　①　　　②

感想例

ひき算も１つの式にできた。
ひき算は、計算の順番が大切だ。

板書例とワークシート

イラスト／横井智美、やひろきよみ

【関連記事】

文部科学省教科調査官監修｢教科指導のヒントとアイデア｣シリーズはこちら！

>>もっと見る

小学館IDをお持ちの方はこちら

初めてご利用の方