小5算数「図形の角」指導アイデア《図形の角の大きさに着目し、三角形の内角の和について発展的に考える》
執筆/横浜市立つつじが丘小学校教諭・山田薫
監修/文部科学省教科調査官・笠井健一
島根県立大学教授・齊藤一弥

目次
単元の展開
第1・2時(本時)図形の角の大きさに着目し、二等辺三角形の内角の和について、帰納的に考える。図形の角の大きさに着目し、三角形の内角の和について発展的に考える。
▼
第3時 三角形の内角の和に着目し、四角形の内角の和について、演繹的に考える。
▼
第4時 図形の角の大きさに着目し、多角形の内角の和について、演繹的に考える。
▼
第5時 内角の和に着目し、一般四角形の敷き詰めについて演繹的に考える。
本時のねらい
三角形の角の大きさについて様々な三角形をかいて帰納的に考察し、内角の和の性質を見いだし、説明することができる。
評価規準
様々な三角形の3つの角の大きさに着目して、内角の和の性質を見いだし、説明している。
本時の展開

直角三角形の角の大きさを調べよう。
この三角形の角の大きさを調べてみましょう。
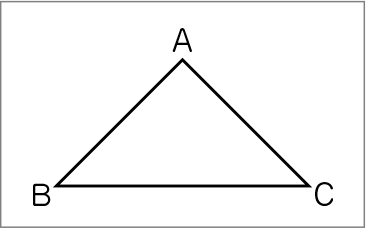
二等辺三角形っぽい。
1つだけ、測らなくても分かる。
うん。直角三角形だから、角Aは90°。
残り2つは……、角Bと角Cは45°。
※点Aを上に伸ばす。
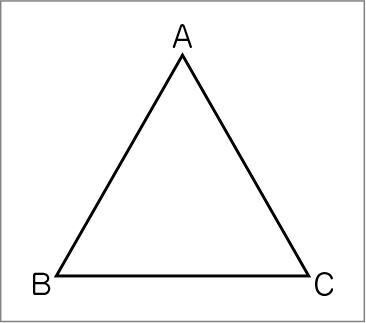
おおお! 三角形の形が変わった。
うん。変わった。
どう変わりましたか。
角Aは小さくなって、角Bと角Cは大きくなっています。
この三角形の角の大きさを調べてみましょう。
角Bと角Cは60°。角Aも60°になった。
これは正三角形だね。
さらに伸ばしてみますね。
※点Aをさらに上へ伸ばす。
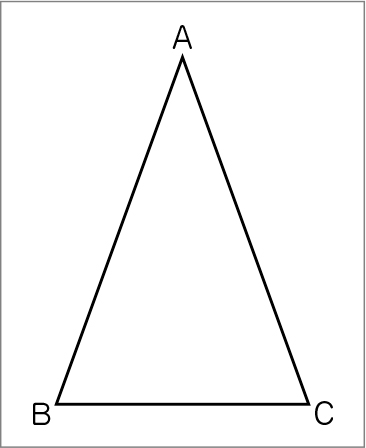
また角Aが小さくなった。
二等辺三角形ということは変わらなそうだけど……。
そして、やっぱり角Aは小さくなって、角Bは大きくなっている。
何度だろう。
もう測ったよ。角Aは20°で、角Bは70°。
先生。これはきまりがありそうです。
三角形の角の大きさには、何かきまりがあるのでしょうか。
ありそうです。
それでは、三角形の角の大きさには、何かきまりがあるのか考えてみましょう。
※一旦の共有。
何かきまりは見付かりましたか。
3つの角をすべて足すと、180°になりました。
うん。なった。
ということは、どんな三角形でも3つの角の和は180°になるのでしょうか。
たまたまかもしれない。
今回は二等辺三角形しか調べてない。他の三角形でも言えるのかな。
きちんと調べてみないと分からないね。
どんな三角形でも、3つの角の和は180°になるのか、三角形をかいて調べてみよう。

三角形の角の大きさには何かきまりがあるのか、考えよう。
見通し
正三角形や直角三角形でも言えるのか、調べたらできそうだな。(方法の見通し)
二等辺三角形でも正三角形でもない、たまたまかいた三角形でも言えるのか調べてみたいな。(方法の見通し)
三角形の3つの角の和は180°になりそうだな。どんな三角形でも言えそう。(結果の見通し)
自力解決の様子
A つまずいている子
どんな三角形をかいたらよいか分からず、教師の支援がないと考えることが難しい。
B 素朴に解いている子
二等辺三角形だけでなく、正三角形や直角三角形など、既習の三角形をかいて、角を測って調べている。
C ねらい通り解いている子
たまたまかいた三角形でも、角を測ったり、3つの角を切り離して角をくっつけたりして、調べている。
学び合いの計画
本学習は、この後の学習に四角形……と発展していく際の根拠となる学習です。例えば、単元計画上で、第3時には、三角形の内角の和を基にして、四角形の内角の和を考え、説明する活動を扱います。第4時には、五角形や六角形の内角の和の求め方を考え、説明する活動を扱います。そこには、本時で行う、三角形の内角の和は180°であるということを根拠に子供たちは説明をしていきます。
そこで、本時の学習では、提示された三角形だけではなく、既習の正三角形や直角三角形でも言えるのか、また、たまたま自分でかいた三角形でも言えるのかと、帰納的に考察する態度を育てていきましょう。そして、内角の和が180°であるという性質が、「どのような三角形でも言える」ということをていねいに扱っていきましょう。その経験が、「四角形でも何かきまりがあるのか?」「多角形の内角の和はどうやったら求められるのか?」「多角形の内角の和にもきまりがあるのか?」と、絶えず考察の範囲を広げていく意欲につながっていきます。分かったことや子供自身が見いだしたことを教師が価値付け、ふり返っていくことで、そのような態度を醸成していきましょう。
考えの共有の場面では、1人1台端末の活用が有効となります。始めに提示された二等辺三角形以外の二等辺三角形を考察している子供は、より一般性を求めて考察しています。また、正三角形や直角三角形、たまたまかいた三角形など、様々な三角形について考えている子供はより考察の範囲を広げて考えています。子供自身が、どのような目的でその考えに至ったのかを、端末上でも分かるように見える化していくこと、そして子供がそれぞれ考えたことを、教師が価値付けることなど、単なる考えの共有にとどまらない工夫が必要です。
ノート例
A つまずいている子

B 素朴に解いている子

全体発表とそれぞれの考えの関連付け
※C1、C2のそれぞれが発表をする。
C1
他の二等辺三角形をかいて、角を測ったら、3つの角の和は180°でした。
C2
直角三角形をかいて角を測ったら、90°と30°と60°でした。なので、3つの角の和は180°でした。正三角形もかいたのですが、すべて60°だったので、3つの角の和は180°でした。直角三角形も正三角形も、3つの角の和は180°と言えます。
C3
たまたまかいた三角形も180°になるか調べました。角を測る以外にも方法を見付けました。三角形をかいて、角の部分を切りました。3つの角を一点に合わせると、ちょうど直線になりました。ということは180°ということです。
これらの考えを見比べてみて、どんなことが言えそうですか。
イラスト/横井智美

