小１算数「ちがいはいくつ」指導アイデア《お話づくりを通した減法の意味》
執筆／福岡県教育センター指導主事・廣木伸幸
監修／文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
単元の展開
第１時 減法の意味や表し方（求残の場面）
▼
第２時 減法の式の表し方と答えの求め方（求残の場面）
▼
第３時 被減数が10以内の減法計算。減法の意味や式の表し方（求補の場面）
▼
第４時 被減数が10以内の減法計算の練習
▼
第５時 ０を含む減法の計算
▼
第６時 半具体物を使用した求差の求め方
▼
第７時 求差の意味
▼
第８時 （本時） お話づくりを通した減法の意味（評価問題以外）
▼
第９時 お話づくりを通した減法の意味（評価問題）
本時のねらい
減法の式からは、残りの数量の大きさを求める場面や２つの数量の差を求める場面をつくることができることを理解することができるようにする。
評価規準
式を読み取ったり、読み取ったことを言葉や絵に表したりすることができる。（知識・技能）
数量の関係に着目し、式や絵から求残や求補、求差の場面を捉え、お話を考えている。（思考・判断・表現）
本時の展開
これまでの学習をふり返ります。次のお話を式にしましょう。あめを７個持っていました。３個あげました。残りは４個です。どんな式になるでしょう｡（ICTなどを使って提示する）
７－３です。
この後も言えますか。
７－３＝４です。
※子供にとって「式」の認識が、｢＝の前まで」と捉えている子供が多いので、ここでは、｢＝の後まで」含めて式とも言うことを確認しておく。
みなさんはどう思いますか。
７個から、３個あげて、残りが４個になるお話なので、私も７－３＝４だと思います。
そうですね。発表してくれたように､（図１をICTなどを使って提示して）このようなときは、ひき算になりましたね。そして、｢＝の後まで」言うときも、式でした。
（図１）
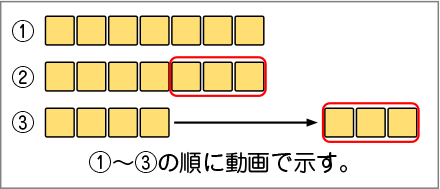
では、今日の問題です｡（問題場面を提示する）
えを 見て、７－３＝４の しきに なる おはなしを つくりましょう。
絵を見て、７－３＝４の式になるお話をつくりましょう。これまでの学習とどんなところが違いますか。
これまでは、お話から式にしたけれど、今日は式からお話にします。
これまでの学習と反対です。
そうですね。では、今日は、どんなめあてで学習をしますか。
７－３＝４になるお話をつくろう。
ひき算の式になるお話をつくろう。
では、めあてを書きましょう。
ひき算の式になるお話をつくろう。
見通し
※見通しは全体で確認します。
はじめに確認したように、７－３＝４の式は､（黒板上で、図１のように数図ブロックを動かしながら）７から３を引いて、４になるということですね。
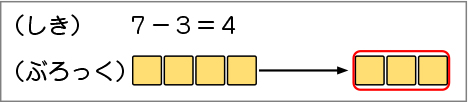
それでは、絵を見てお話をつくりましょう。１つお話ができた人は、７－３＝４の式になる他のお話も考えてみましょう。
自力解決の様子
Ａ つまずいている子
・お話をつくることができない。
「子供が７人いました｡（この先が書けない）」
●３と４に当たるお話が分からない。
●場面とお話を関連付けることができない。
Ｂ 素朴に解いている子
・以下の１つのお話ができた。
子供が７人いました。３人帰りました。残りは４人です。
○７－３＝４の式のお話をつくることができている。
●求差のお話はつくることができていない
Ｃ ねらい通り解いている子
・以下の２つのお話ができた。
子供が７人いました。３人帰りました。残りは４人です。
黄色い花が７輪と、赤い花が３輪咲いています。違いは４輪です。
○求残と求差で７－３＝４の式のお話をつくることができている。
学び合いの計画
自力解決の段階で、１人１台端末を活用して、自分や友達のつくったお話を共有できるようにし、互いのお話を見合うことができるようにしておきます。自他のつくったお話を共有しているので、提出していない子供やＡの子供に対しては個別に指導することができます。特に、Ａの子供に対しては、はじめに絵のなかの７、３、４に当たる数を一緒に確認したうえで、７－３＝４のお話を考えるように促します。
＜自他のお話を共有する方法＞
自分の書いているお話を写真に撮り、共有できるようにデータで提出させる。
全体交流では、まずは、求残になるお話「子供が７人いました。３人帰りました」の部分と、求差になるお話「黄色い花が７輪と赤い花が３輪咲いています」の部分のみを板書上に提示しておき、子供と一緒に続きの部分のお話を確認していきます。その際、Ａの子供に寄り添って「残りは４人です」になるわけを問い、式を根拠に「＝４」となっていることや、７－３の計算の答えの導き方を説明させるようにします。
また、求差の続きについては、｢ここも､『残りは４輪です』でいいよね」のように、誤答を示すことで、求残と求差の違いに気付かせます。さらに、｢子供が７人いました。眼鏡をかけている子供は３人です」と板書し、続きを子供たちと考えることで、求補についても復習をしていきます。
※もし、求補のお話に気付いた子供がいれば、ここで紹介します。事前に互いのお話を見合ったうえで、学び合う時間を設定すると、ＢやＡの子供は正しいお話や考えていなかったお話に気付きやすくなります。Ｃの子供も、他の表現をしているお話（お話づくりは表現の仕方が多様にある）に触れることで、友達の考えを解釈し、考えの根拠を読み取る経験を積むことができます。
ノート例
※赤字で書かれている箇所は、解決方法の共有や交流のなかで、付加・修正して書いたものです。
Ａ つまずいている子
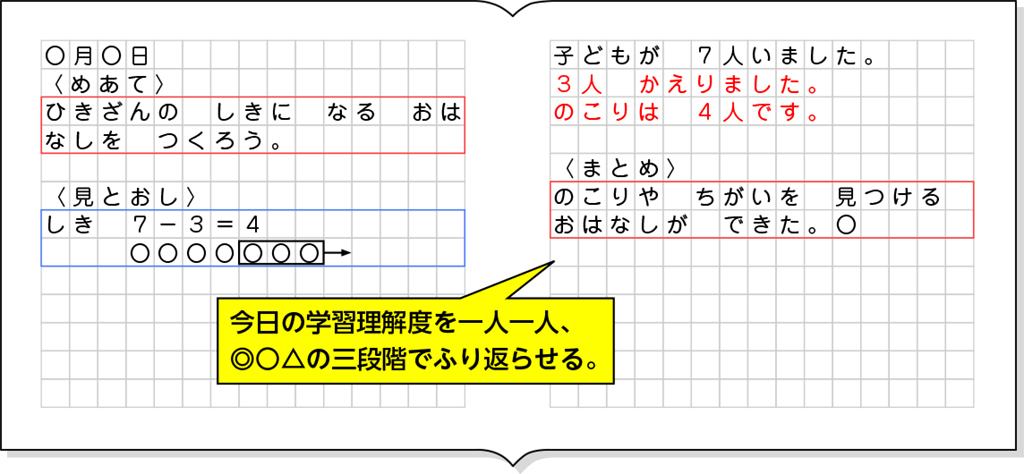
Ｂ 素朴に解いている子
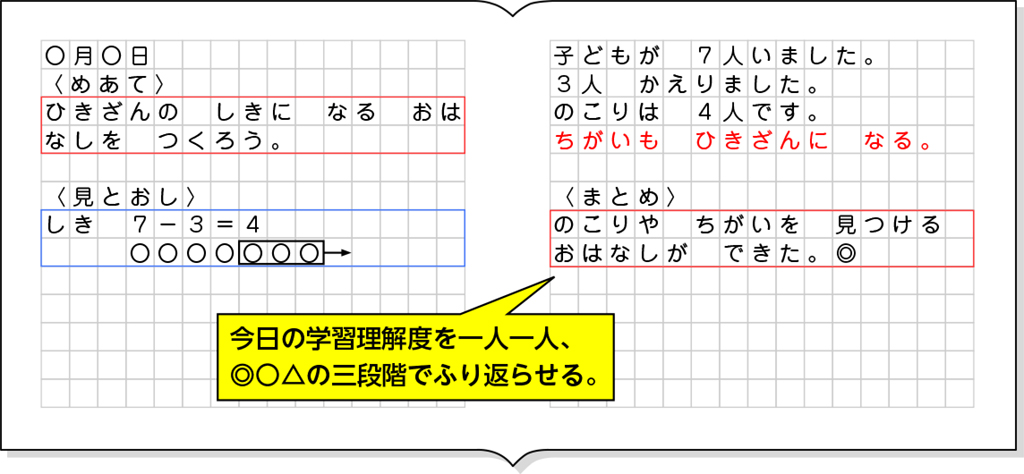
全体発表とそれぞれの考えの関連付け
※求残になるお話「子供が７人いました。３人帰りました」の部分と、求差になるお話「黄色い花が７輪と赤い花が３輪咲いています」の部分のみ、板書上に掲示しておく。
【求残のお話について】
黒板には、｢子供が７人いました」と書いていますが､（ICTを使って子供のつくったお話をいくつか提示して）｢人が７人いました」や、｢お兄さんとお姉さんが７人いました」のようなお話にしてもよいですよね。
はい。７人いることは同じなのでよいです。
そうですね。お話の続きに「３人帰りました」と書きましたが、なぜ、先生がこのようなお話にしたと思いますか。
絵のなかの（絵を指して）７人のなかで、３人が帰っているからだと思います。
７－３＝４の式の「－３」のお話にしたいからだと思います。
先生の気持ちがよく分かりましたね。先生は「－３」のお話にしたかったので、絵のなかの３人が帰っているところをお話にしました。そして、｢３人帰りました」のところも､（ICTを使って子供のつくったお話をいくつか提示して）｢あとで、３人帰りました」や、｢３人帰ると」のようなお話にしてもよいですよね。
はい。３人減っていることが同じなのでよいです。
そうですね。式にするときは、１つの式に決まることが多いけれど、式をお話にすると、いろんなお話ができるんですね。では、｢子供が７人いました。３人帰りました」のお話の続きは、どのようになりますか。
残りは４人です。
残りは４人になりました。
すばらしい！ どちらもよいですね。それでは、この式から「残りは３人になりました」というお話もできますか。
それはいけないと思います。
なぜですか。
式が、｢７－３＝４」だから、｢残りが４」の「４」は変えてはいけません。
もし「残りが３人」なら、｢７－３＝３」で間違った式になります。
なるほど。式をお話にすると、いろんなお話ができるけれども、式で使っている数は違ってはいけないのですね。それでは、｢子供が７人いました。３人帰りました」のお話の続きは、｢残りは４人です」と黒板には書いておきますね。
【求差のお話について】
次に、お花に注目していた友達もいましたよ。｢黄色い花が７輪と赤い花が３輪咲いています」というお話です。でも、なぜ「お花が10輪咲いています」というお話にしなかったのでしょう。
「７－３＝４」の式に「10」がないからです。
そうでした。｢７－３＝４」の式でしたね。では、｢黄色い花が７輪と赤い花が３輪咲いています」のお話の続きですが、先生は分かりましたよ。
どうなるのですか。
さっきのお話と同じように、｢残りは４輪です」ですね。
あれ。そうかな。
みなさん何か言いたそうですね。お話の続きが「残りは４輪です」でよいか、隣の友達とお話ししてみましょう。
※隣と相談する時間をとる。
それでは、お話の続きが「残りは４輪です」でよいか、発表しましょう。
減ってないから「残り」ではないと思います。
私もよくないと思います。お花のお話は、｢違い」はいくつかを言わないといけないです。
なるほど、｢残りはいくつ」と「違いはいくつ」では、違いがありましたね。この違いを図やブロックで説明できる人はいますか｡（黒板上で求残と求差の違い（図２）を説明させる）
（図２）
説明してくれたように、お花のお話は、｢残り」ではなく、同じ数を数えない「違い」を見付けるお話ですね。では、どのようなお話の続きがいいですか。
違いは４輪です。
黄色い花が４輪多いです。
すばらしい。どちらもよいですね。それでは、｢黄色い花が７輪と赤い花が３輪咲いています」のお話の続きは、｢違いは４輪です」と黒板には書いておきますね。
【求補のお話について】
※求補のお話に気付いた子供がいれば、ここで紹介する。
実は、この絵にはもう１つ「７－３＝４」になるお話がありますよ。子供が７人いました。眼鏡をかけている子供は……。
３人います。
そうですね｡（｢子供が７人いました。眼鏡をかけている子供は３人です」と板書する）このお話の続きはどうなるでしょう。隣の友達とお話ししてみましょう。
※隣と相談する時間をとる。
それでは、お話の続きを発表しましょう。
残りは４人です。
残りの子供は４人です。
ここでの「残り」とは、どんな子供のことですか。
眼鏡をかけていない子供です。
それなら、｢眼鏡をかけていない子供は４人です」のほうがいいかな。
そうですね。みんなが気付いたように、このお話は、｢残り」のお話ですね｡（図３のように黒板で図やブロックを使って説明する）でも、｢残り」と言っても、｢眼鏡をかけていない子供」ということは分かりにくいですね。そんなときは、｢めがねをかけていない子供は４人です」のようなお話のほうがよいですね。
（図３）
【まとめに向けて】
今日は、どんなお話ができましたか。
｢残り」のお話です。
｢違い」を見付けるお話です。
※この後、この発表を基に学習のまとめをする。
学習のまとめ
※「全体発表とそれぞれの考えの関連付け」のやりとりのポイントを黒板に残し、それを使ってまとめをする。
今日のめあては、｢ひき算の式になるお話をつくろう」でした。まとめを発表しましょう。
残りや違いを見付けるお話ができた。
※ここまでが第８時
評価問題
※この評価問題は第９時に行う。
ひきざん え本を つくりましょう。
※下のような見本を示します。画用紙１枚で作成します。何種類作ってもよいです。
子供に期待する解答の具体例
〔求残の例〕…評価問題の手本
〔求差の例〕
〔求補の例〕
感想例
- ひき算には「残り」のときと「違い」のときがある。
- 同じ式からいろいろなお話ができた。
ワークシートと板書例
イラスト／横井智美、やひろきよみ
