小５算数「小数のわり算」指導アイデア《数直線で「除数が小数の除法」の意味を捉える》
執筆／横浜市立庄戸小学校教諭・渡邊督之
監修／文部科学省教科調査官・笠井健一
島根県立大学教授・齊藤一弥
目次
単元の展開
第１時（本時）問題場面の数量の関係を数直線に表し、除数が小数の除法の意味を捉える。
▼
第２時 除法に関して成り立つ性質を使って、整数÷小数の計算の仕方を考える（除数が１より大きい場合）。
▼
第３時 除法に関して成り立つ性質を使って、整数÷純小数の計算の仕方を考える（除数が１より小さい場合）。
▼
第４時 除法に関して成り立つ性質を使って整数の除法にし、小数÷小数の計算の仕方を考える。
▼
第５・６時 除法に関して成り立つ性質を使って整数の除法にし、小数で割る筆算の仕方を考える。
▼
第７時 被除数を変えずに除数の数を変えたときの商を比較し、除数と商の大きさの関係を理解する。
▼
第８時 除法に関して成り立つ性質を使って筆算し、余りがある場合の小数で割る除法の計算の仕方を考える。
▼
第９時 除法に関して成り立つ性質を使って筆算し、商を概数で表す方法を知る。
▼
第10・11時 問題場面の基準量と比較量の関係を数直線に表し、倍を表す小数や比較量の求め方を考える。
▼
第12時 問題場面の基準量と比較量の関係を数直線に表し、基準量の求め方を考える。
本時のねらい
除数が小数の場合の立式について、乗法の逆であることや整数の除法・被除数が小数の場合の除法を基にして、数直線を使って説明する。
評価規準
除数が小数の場合の立式について、乗法の逆であることや整数の除法・被除数が小数の場合の除法を基にして、数直線を使って説明することができる。（思考・判断・表現）
本時の展開
リボンを2.5ｍ買ったら、代金は300円でした。このリボン１ｍのねだんは何円ですか。
今日もみんなで新しい問題を考えましょう。１ｍの値段が120円のリボンを2.5ｍ買いました。代金はいくらですか。
あれ？ なんだか見たことあるなぁ。
この問題、前に学習しました！（教室に掲示してある小数のかけ算の学習の模造紙を指さす）
先生、新しくありません。
おや？ そうでしたか。いけない、いけない。教えてくれてありがとう。ちなみに、この問題の式はどうやって考えたのでしたか。
数直線を使って説明しましたよ。
数直線にして、２年生のときの考え方で「１つ分の量」が120円、｢いくつ分の量」が2.5ｍ、｢全部の量」が□円だから、120×2.5＝□と考えました。
でも、｢いくつ分の量」が2.5というのは変だから、2.5倍と考えたよね。
数直線は上も下も比例して2.5倍と考えたよ。
120×2.5＝□の□には何が入りましたか。
300が入りました。だから答えは300円でした。
みんな、よく学習していますね。□の中に300と書いておきますね。では、改めて新しい問題です。今度は間違えないようにしますね。１ｍの値段が120円のリボンを、ある長さだけ買ったら、代金は300円になりました。買った長さは何ｍですか。
えっ？ これも新しくない……。
かけ算かな。わり算かな。
何算か分からないときはどうしたらいいでしょうか。
数直線を使うといいです。
では数直線に、分かっていることと聞かれていることを表しましょうか。
１ｍの値段が120円だから、｢１つ分の量」が120円。数直線の１の上が120になります。
買った長さが分かっていないから、｢いくつ分の量」が□。数直線の１（ｍ）の右側に□を書きます。
全部の代金が300円だから、｢全部の量」が300円。数直線の□の上が300になります。
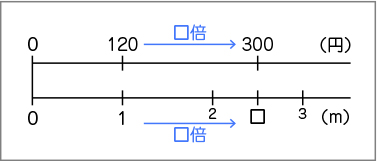
数直線を見たら120×□＝300になるから、□を求める式は、300÷120＝□になるね。
あれ？ これ習ったことあるから新しい問題じゃないよ。
先生！ しっかりしてください。
おや？ そうでしたか。いけない、いけない。また教えてもらいましたね。ちなみに、300÷120はいつ習ったのでしたか。
４年生のとき習いましたよ。
計算したら、300÷120は2.5になりました。だから答えは2.5ｍです。
では、□の中に2.5と書いておきますね。
あれ？ 数直線がかけ算のときと同じだ。
本当だ！
あら偶然！ 不思議なこともあるものですね。今度こそ、新しい問題です。リボンを2.5ｍ買ったら代金は300円でした。このリボン１ｍの値段は何円ですか。
これは１ｍの値段が分かっていないから、わり算だよ。
あれ？ これも前の２つと同じ数直線になるんじゃないかな……。
今回は１ｍの値段が分かっていません。小数が入っているけれど……。
わり算だよ！ 今まで習ったことと同じ！
数直線にすると分かるよ！
では、どんな式になるか、数直線を使って考えてみましょうか。
どんな式になるか、数直線を使って説明しよう。
見通し
今までの数直線と同じように、分かっていることを数直線に表してみよう。（方法の見通し）
１ｍの値段が分かっていないから、数直線の１の上が□になるな。（方法の見通し）
｢全部の量」が分かっているから、わり算の式になりそう。（結果の見通し）
自力解決の様子
A つまずいている子
既習である、かけ算のときや整数のわり算のときの数直線を基にすることができず、教師の支援がないと考えることが難しい。
Ｂ 素朴に解いている子
かけ算のときや整数のわり算のときの数直線を基にして、新たな問題場面を表した数直線を用いて立式している。
Ｃ ねらい通り解いている子
問題場面を表した数直線を用い、比例の関係や「１つ分の量」など三項の関係を使って立式の根拠を説明している。
学び合いの計画
本単元では、除数が小数である場合まで数の範囲を広げて、除法の意味を捉え直すことがねらいの１つとなっています。除法の意味として、乗法の逆であることや、包含除（いくつ分の量を求める場合）と等分除（１つ分の量を求める場合）の２つの場合があることを学習してきています。
その意味を全体で確認し、数直線や式に表しておくことで、除数が小数である場合まで数の範囲を広げる際に、数直線というツールで統合的に見ることができるようになるのではないかと考えます。統合的に見ることで一人一人が自分の解決策をもつことができ、ペアで考えを伝え合ったり、全体に自分の考えを伝えたりするときに、主体的に取り組むことができると考えています。よって、主体的に学び合いを行うためにも、除法の意味を改めて捉えさせておくことは重要だと考えます。
全体発表の前にペアで考えを伝え合った後、タブレット端末で自分の考えを写真に撮って提出させ、全員の考えをモニター画面に映します。その画面を全体で見ながら、それぞれの考えの「同じところ・違うところ」で仲間分けしていきました。
ノート例
Ｂ 素朴に解いている子
Ａ つまずいている子
全体発表とそれぞれの考えの関連付け
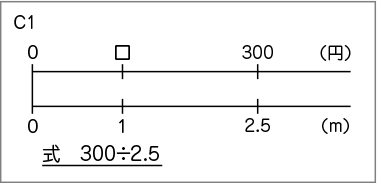
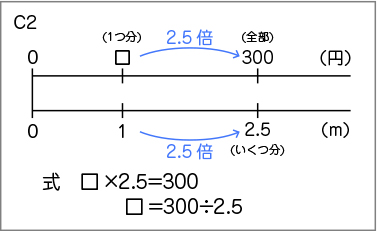
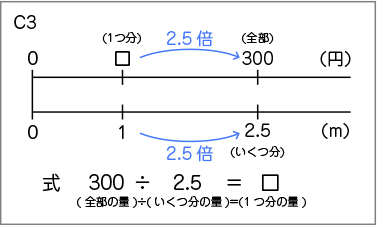
みんな、数直線に表すことができていましたね。テレビ画面に映っているなかで、Ｃ１さんとＣ２さんとＣ３さんの考えを黒板に取り上げました。
私は、Ｃ１さんと同じ考えをかいたよ。
僕は、Ｃ２さんと似ている。
みなさんはどうですか。Ｃ１さんと同じような考えをかいた人、手を挙げてください。
※挙手する。
あれ？ 〇〇さんは手を挙げていないけれど、この考えと同じでしたね。
あ、そうだ！（挙手）
Ｃ２さんと同じような考えをかいた人、手を挙げてください。
※挙手する。
今、手を挙げてくれた人は、Ｃ１さんの考えと違うところはどこですか。どちらも正しく数直線に表すことができているけれど。
数直線の下が2.5倍になっていて、上も比例しているから2.5倍と書きました。
数直線を見たらかけ算のときと同じだったので、□を使った式にしてからその反対で考えました。
かけ算の場合を基にして考えたのですね。これまでの学習がよく身に付いていてすごいです。Ｃ３さんと同じような考えをかいた人、手を挙げてください。
※挙手する。
今、手を挙げてくれた人は、Ｃ２さんの考えと違うところはどこですか。こちらも数直線は同じですね。
数直線を見たら、｢いくつ分の量」と「全体の量」が分かっていて、｢１つ分の量」が分かっていないから、｢全体の量」÷「いくつ分の量」＝「１つ分の量」になると今まで習ったことを使ったところです。
〈Ｃ１〉私も書いていないけれど、同じように考えていました。
みんな、今まで学習したことを上手に使って説明することができましたね。すごいです。
学習のまとめ
数直線を使って式を考えてきたけれど、今日の学習でよかったところはありますか。
数直線に表したら、かけ算のときと同じ考え方で式が分かりました。
数直線を使ったら、｢１つ分の量」と「いくつ分の量」と「全部の量」が分かって、今まで通りに式が立てられました。
数直線の下が2.5倍だから、上も比例して2.5倍になると分かって、□を使って式が立てられました。
これまでも学習してきたけれど、数直線を使うとよいことがまた分かりましたね。みんなの言ってくれたよさを、まとめて書きますね。
数直線を使うと、比例やかけ算の式にしたり、｢１つ分の量」｢いくつ分の量」｢全部の量」が分かったり、□を使った式にしたりして、どんな式になるか説明できる。
評価問題
※ここでは、｢１つ分の量」が分かっていない等分除が、わり算の典型例として固定しないよう、あえて「いくつ分の量」が分かっていない包含除の場面の評価問題を出しています。導入で包含除の場面にはふれているので、それを活用できるよう支援するとよいです。
10ｍのリボンを１人に2.5ｍずつ配ります。何人に配れますか。数直線と式で表しましょう。
子供に期待する解答の具体例
式 2.5×□＝10
□＝10÷2.5
感想例
- 数直線に表すと、（１つ分の量）が分からないときも、いくつ分の量が分からないときも、式が立てられるようになるから便利だと思いました。
- 割る数が小数のときも数直線に表して、上も下も何倍と考えたら、かけ算のときの反対で考えられるから、かんたんだと思った。
- 数直線を見たらかけ算のときと同じだと思ったし、□を使った式にしたらかんたんにわり算だと思ったから、今まで習ったことを使って考えるのは大切だと思いました。
ワークシートと板書例
イラスト／横井智美
