小3算数「かけ算の筆算2けた」指導アイデア《2位数×2位数(部分積がみな2桁で繰り上がりなし)の計算の仕方》

執筆/東京都目黒区立八雲小学校教諭・菊地めぐみ
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時 1位数×何十の計算の仕方
▼
第2時 2位数×何十の計算の仕方
▼
第3時(本時)2位数×2位数の計算の仕方(12×23)
▼
第4時 2位数×2位数(12×23)の筆算の仕方
▼
第5時 2位数×2位数の計算の仕方(58×46)、繰り上がりあり
▼
第6・7時 3位数×2位数の計算の仕方、筆算の仕方
▼
第8時 簡単な場合の2位数×1位数の暗算の仕方
▼
第9時 十進位取り記数法及び筆算の仕組みのよさを感得する。
▼
第10時 学習内容の習熟を図り、活用した見方・考え方をふり返る。
本時のねらい
2位数×2位数(部分積がみな2桁で繰り上がりなし)の計算の仕方を、これまでの学習を基に説明することができる。
評価規準
2位数×2位数の計算の仕方について、これまでの学習を基に数の構成に着目して説明している。
本時の展開
※前時までの「何十を掛ける計算」での学習感想を取り上げて、本時の課題につなげる。
昨日は「何十を掛ける計算」について学習しましたね。学習感想で「ぴったりじゃない数を掛けるときにはどう計算するか考えたい」と書いた人がいました。「ぴったりじゃない」とは、どういうことでしょうか。
昨日は、5×30や12×40など、掛ける数が切りのいい数でした。
5×31など、一の位が0ではない数を掛ける計算がぴったりじゃないということだと思います。
ぴったり、何十という数でなくても、計算できるでしょうか。こんな場面で考えてみましょう。

1まい12円の工作用紙を □まい買います。代金はいくらですか。
□に入る数が、昨日までだと…‥。
10や20、30、40など、ぴったりの数です。
そうですね。では、今日は『23まい』に挑戦してみましょう。代金を求める式を立ててみましょう。
12×23です。「1枚の値段」×「買う数」=「代金」だからです。
たし算だと、12+12+12+12……、と12を23回足すことになります。これはかけ算で12×23と表せます。
テープ図だと、20枚の少し先、23枚のところの値段を求めることになります。
昨日とは違って「何十」を掛けるわけではないけれど、代金を求めることができそうですか。

何十ぴったりではない2桁の数を掛ける計算の仕方を考えよう。
見通し
答えは、どれくらいになりそうですか。
掛ける数が20ならば、昨日までの計算で求められます。それより少し多いから……。
20枚の計算をみんなで計算してみましょう。
12×20=12×2×10=24×10=240。240円より少し多い金額になるはずです。
自力解決の様子
A つまずいている子
・23が20と3で構成されていることに気付いていない。
・形式だけの筆算をしている。(12×2=24と12×3=36を組み合わせるなど)
B 素朴に解いている子
・23を20と3に分けて計算する式が書ける。
12×20=240 12×3=36
240+36=276
C ねらい通り解いている子
・式の意味を言葉で説明できている。
12×20=12×2×10=24×10=240
12×3=36
240+36=276
23を20と3に分ける。20枚の値段は240円、3枚の値段は36円。合わせて276円。
・位ごとの計算を図のように表現している。
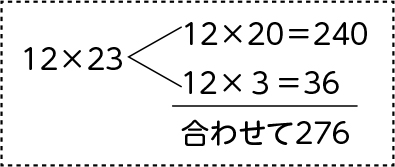
自力解決の様子から、子供たちの状況を評価します。20を掛ける計算をどのように生かして、23を掛ける計算に向かえばよいか、全員が考えられるように、23をどう扱ったかに注目させる指導を行います。
学び合いの計画
- 掛ける数の23について、どのように工夫して代金を求めているかに注目してノート展覧会を行う。
→23を20と3に分けている子供が多いことに気付くことができるようにする。 - ノート展覧会のあと、自分のノートに追加で説明を書き加える時間をとる。
- 自力解決で形式だけの筆算になってしまった子供が、23を20と3に分けることで、これまでの学習が使えることに気付いているかに注目して学び合いの活動を見守り、友達のノートを見る視点などについて、必要があれば助言する。
ノート例
B 素朴に解いている子

イラスト/横井智美

