小4算数「直方体と立方体」指導アイデア《平面上や空間にある点の位置の表し方について理解する》

執筆/横浜市立獅子ケ谷小学校教諭・真島慎也
監修/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥

目次
単元の展開
第1時 身の回りの箱の形に関心をもち、既習の平面図形を基に直方体や立方体、立体の意味について理解する。
▼
第2時 構成要素に着目して、直方体や立方体の特徴、性質を理解する。
▼
第3・4時 辺の長さや面のつながりなどに着目して、直方体、立方体の展開図をかき、直方体や立方体の特徴を説明する。
▼
第5時 直方体の面と面の垂直、平行の関係を理解する。
▼
第6時 直方体の辺と辺の垂直、平行の関係や、面と辺の垂直、平行の関係を理解する。
▼
第7時 直方体、立方体の見取図をかく。
▼
第8時(本時)平面上や空間にある点の位置の表し方について理解する。
▼
第9時 学習内容を確認し、数学的な見方・考え方をふり返る。
本時のねらい
平面上にある点の位置の表し方を基にして、空間上にある点の位置の表し方を考える。
評価規準
空間上にある点の位置の表し方について、基にする点からの3つの長さの組で表す方法を考えている。
本時の展開

点Bと点Cは、どこにあると言えばよいだろうか。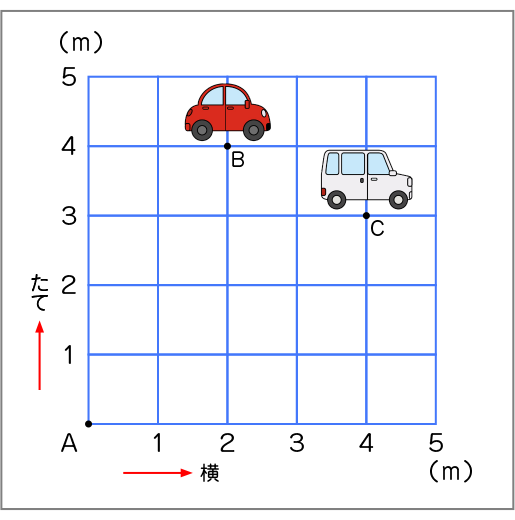
2台の車は、どの位置にあると言えばよいでしょうか。
どこから出発したのか知りたいです。
Aから出発しているなら、まっすぐ進んでBまで来たということでしょうか。
もし道路だったら、縦か横にまっすぐ進んで1回曲がります。
Bは縦4m、横2m進んだことになります。
Cは縦3m、横4m進んだことになります。
点の位置を表すときは、点Aを基にすると、点Bは(横2m、縦4m)と表すことができます。
今どこにいるのかということが分かりました。
点Cは(横4m、縦3m)と表すことができます。
進み方ではなく、今いる位置を表すことができました。
車だとどこにいるかだけですが、物を棚に置くときなどには、どのように表せばよいのでしょうか。
車に風船をつけて走らせたときに、風船の位置は、どの位置にあると言えばよいでしょうか。

点Eと点Fは、どこにあると言えばよいだろうか。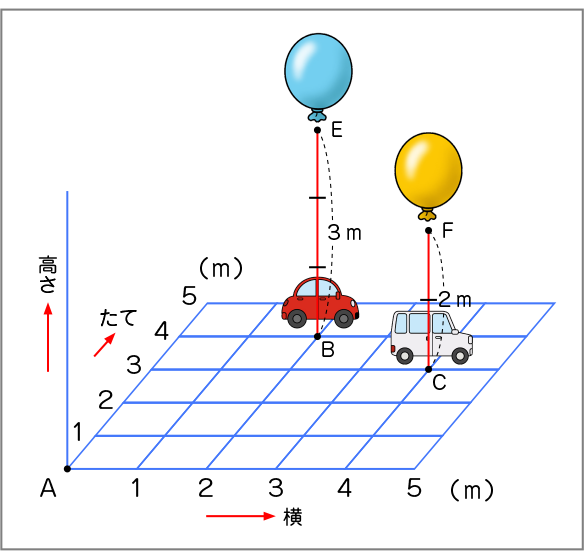
空中にあるときは、どのように表せばよいのだろう。
平面のときは、縦と横を使ったから。
Bの車の風船は、Bの車の真上にあるということ。
Cの車の風船は、Cの車の真上にあるということ。
これも基にする点が必要ということかな。
風船は車の真上にあります。点Aを基にすると、縦と横の長さは変わるでしょうか。
まだ分かりません。
縦と横の長さは変わらないと思います。
でも、縦と横だけだと、どこに風船があっても同じになってしまいます。
空間にある点の位置の表し方を考えて、説明してみましょう。

空間にある点の位置の表し方を考えて、説明しよう。
見通し
平面のときは、縦と横の2種類を使って表した。だから、もう1つ数字を使えばよいのではないか。(方法の見通し)
点Aや点Eや点Fが直方体の頂点のように見えてきたな。まだ使っていない高さを使えば、点Eは高さ3mだ。(結果の見通し)
自力解決の様子
A つまずいている子
空間にある点の位置の表し方が分からない。高さのみで表している。
B 素朴に解いている子
平面上の点の位置と高さを個別に書き、空間にある点の位置を表している。
C ねらい通り解いている子
平面上の点の表し方を基に、横、縦、高さを用いて、空間にある点の表し方を考え、説明している。
学び合いの計画
平面上にある点の位置を表す際に、基にする点を決めることとその点から2方向の長さを用いることで、すべての平面上にある点の位置を表現できることを学んでいます。そのことをふまえ、空間にある点の位置はどのように表せばよいか、直方体と立方体の特徴を想起させながら学習を行っていきましょう。
空間にある点の位置は、平面上にある点の表し方だけでは、高さによる表現の違いが出ないことや、3方向の長さを用いることで、位置を表せるのではないか、といったような意見交換する活動を通して、平面や空間の認識をより深いものとし、座標平面や座標空間といった数学的な見方を養うことができると考えます。
ノート例
B 素朴に解いている子
イラスト/横井智美、やひろきよみ


