小４算数「分数」指導アイデア《同分母分数のたし算とひき算の理解》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.02.28

単元の展開

第１時　単位分数を基に、さまざまな分数を捉え、真分数や仮分数、帯分数の表し方や意味を理解する。
▼
第２時　数直線を基にして、真分数や仮分数、帯分数の大小比較をし、分子が同じ分数分母が大きいほど小さくなることを理解する。
▼
第３時　数直線や単位分数を基にし、仮分数を帯分数になおす方法を考え、説明する。
▼
第４時　数直線や単位分数を基にし、帯分数を仮分数になおす方法を考え、説明する。
▼
第５時　数直線を基にして、分数の大小比較をし、分子が同じ分数は分母が大きいほど小さくなることを理解する。
▼
第６時（本時）問題場面を捉え、数直線を基に同分母分数のたし算とひき算の計算の仕方を理解する。
▼
第７時　問題場面を捉え、数直線を基に帯分数のたし算の演算決定を理解する。
▼
第８時　問題場面を捉え、数直線を基に帯分数のひき算の演算決定を理解する。
▼
第９時　学習の内容を確認し、数学的な見方・考え方をふり返る。

本時のねらい

単位分数に着目して、同分母分数の加減計算の仕方を整数の加減計算を基に考え、説明することができる。

評価規準

単位分数の個数に着目し、同分母分数の加減計算の仕方を考え、説明している。

本時の展開

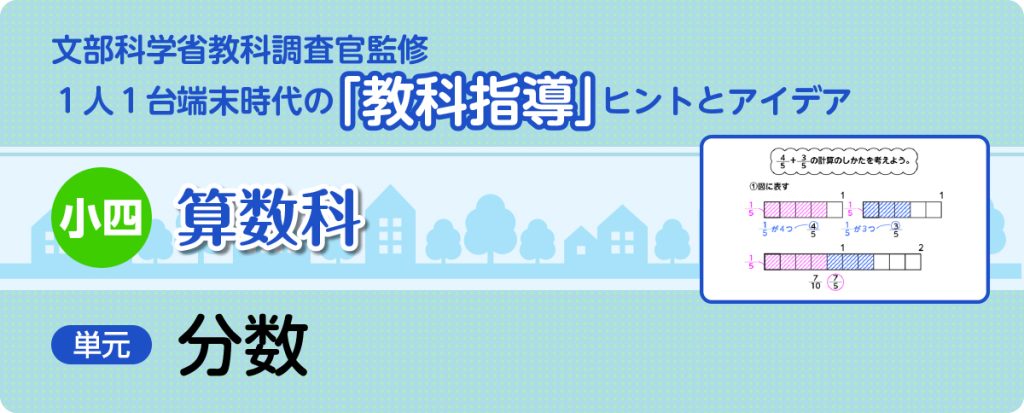
[MATH]\(\frac{4}{5}\)[/MATH]ｍと[MATH]\(\frac{3}{5}\)[/MATH]ｍのテープを合わせると何ｍになりますか。

たし算をすればいいんだ。

どのような式になりますか。

[MATH]\(\frac{4}{5}\)[/MATH]＋[MATH]\(\frac{3}{5}\)[/MATH]です。

どのように計算していきますか。

でも、分数どうしを足すことはできるのかな。

どうすれば、分数どうしを足すことができますか。

図に表します。数直線に表します。[MATH]\(\frac{1}{5}\)[/MATH]が何個分かを基にして考えます。

整数のときのように、40＋30のときには、10を基にして４＋３をすればできたので、分数でも使えないかな。

小数のときも、0.4＋0.3のときには、0.1を基にして４＋３とできたので、分数でも使えないかな。

そうですね。今まで学んできた、整数＋整数や小数＋小数の考え方を参考にしていくと、どのように分数＋分数の計算をしていくのか考えられそうですね。分数のたし算の仕方を考えてみましょう。

分数＋分数の計算の仕方を考えよう。

見通し

[MATH]\(\frac{1}{5}\)[/MATH]を基にすることで、４＋３の計算で答えを求めることができそうだな。（方法の見通し）

図や数直線に書き表すと計算の仕方が分かりそうだね。（方法の見通し）

式から同分母であることに気付き、[MATH]\(\frac{1}{5}\)[/MATH]を基に計算ができ、和は１より大きくなることを考える。（結果の見通し）

自力解決の様子

Ａ　つまずいている子
分母どうし、分子どうしを足して、[MATH]\(\frac{7}{10}\)[/MATH]と考えている。

Ｂ　素朴に解いている子
図や数直線を使って考えている。

Ｃ　ねらい通り解いている子
同分母分数であることに着目し、整数＋整数や小数＋小数の考え方のときのように、[MATH]\(\frac{1}{5}\)[/MATH]を基にして４＋３＝７。[MATH]\(\frac{1}{5}\)[/MATH]が７個分で、[MATH]\(\frac{7}{5}\)[/MATH]であると考えている。

学び合いの計画

分数の加法と減法の指導では、和が１より大きい同分母分数の加法及び減法の計算の仕方を形式的に理解することをゴールにするのではなく、単位分数の個数に着目すれば整数の加法及び減法の求めることを理解できるようにしましょう。

そのために、分数が同分母であることに着目させ、図や数直線から[MATH]\(\frac{1}{5}\)[/MATH]が基になっていることを確認していくことが大切です。

図や数直線を扱う際には、[MATH]\(\frac{4}{5}\)[/MATH]と[MATH]\(\frac{3}{5}\)[/MATH]を合わせた数が「図や数直線のどの部分に当たるのか」や「１がどこか」ということをていねいに確認する必要があります。

そして、[MATH]\(\frac{1}{5}\)[/MATH]が単位になっていることを図や数直線を基に捉え、整数どうしのたし算として見れることを理解させていきましょう。

この考え方は、整数や小数の加法、減法の計算と同じです。同分母分数の場合も単位分数に着目することで、同じ様に計算の仕方を統合的に捉え、既習事項を基に計算の仕方を導き出していく子を育てましょう。

５年生で行う、異分母分数の加法、減法の計算のときにも、単位をそろえることで計算ができるのではないかと自ら問いをもつ子の育成にもつなげていきます。

そのためにも、単位分数を基に計算方法を導き出すことをていねいに指導し、見方・考え方を広げていくことを大切にしていきましょう。

ノート例

Ａ　つまずいている子

Ｃ　ねらい通り解いている子

全体発表とそれぞれの考えの関連付け

※Ｃ１、Ｃ２、Ｃ３のそれぞれが発表をする。

Ｃ１
図で考えました。[MATH]\(\frac{4}{5}\)[/MATH]が左の図、[MATH]\(\frac{3}{5}\)[/MATH]が右の図になります。この２つの色が塗られているところの数を合わせると７つになります。つまり[MATH]\(\frac{1}{5}\)[/MATH]が７つあることを表します。なので、[MATH]\(\frac{7}{5}\)[/MATH]になります。

Ｃ２
数直線で考えました。下のように表すことができました。数直線を数えていくと７つになります。つまり[MATH]\(\frac{1}{5}\)[/MATH]が７つあることを表します。なので、[MATH]\(\frac{7}{5}\)[/MATH]になります。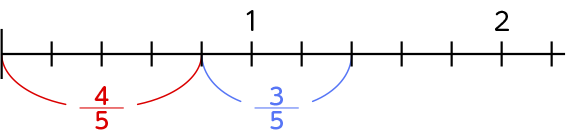

Ｃ３
[MATH]\(\frac{1}{5}\)[/MATH]がいくつ分あるかで考えました。[MATH]\(\frac{4}{5}\)[/MATH]は[MATH]\(\frac{1}{5}\)[/MATH]が４つ分、[MATH]\(\frac{3}{5}\)[/MATH]は[MATH]\(\frac{1}{5}\)[/MATH]が３つ分と表せます。だから４＋３＝７になります。この７は、[MATH]\(\frac{1}{5}\)[/MATH]が７つあることを表しています。なので、[MATH]\(\frac{7}{5}\)[/MATH]になります。10や0.1をもとにしたときと同じです。

どのようにして、計算の仕方を考えましたか。

図を使って考えました。色が塗られているところをすべて数えたら７になったので[MATH]\(\frac{7}{5}\)[/MATH]になると思います。

私は、[MATH]\(\frac{7}{10}\)[/MATH]になると思いました。

何でそう思いましたか。

図をマスの数を数えると10個のマスの中に７個が塗られているから[MATH]\(\frac{7}{10}\)[/MATH]になると思います。

そうですね。[MATH]\(\frac{7}{5}\)[/MATH]と[MATH]\(\frac{7}{10}\)[/MATH]、どちらが正しいのでしょう。

[MATH]\(\frac{7}{5}\)[/MATH]です。

[MATH]\(\frac{7}{10}\)[/MATH]です。

ほかの考え方も見ていきましょう。

数直線を使って考えました。[MATH]\(\frac{4}{5}\)[/MATH]と[MATH]\(\frac{3}{5}\)[/MATH]を足して書き表すと、[MATH]\(\frac{7}{5}\)[/MATH]になりました。

ということは、[MATH]\(\frac{7}{5}\)[/MATH]が正しいのですか。

たぶんそうだと思います。

Ｃ１とＣ２は割られる数を分けて考えているね。

ということは、[MATH]\(\frac{7}{5}\)[/MATH]が正しいのですか。

たぶんそうだと思います。

でも、何で[MATH]\(\frac{7}{5}\)[/MATH]が答えになるのかな。

そうですね。もう１つの考え方を見てみましょう。

私は、[MATH]\(\frac{1}{5}\)[/MATH]がいくつ分あるのかで考えてみました。[MATH]\(\frac{4}{5}\)[/MATH]は[MATH]\(\frac{1}{5}\)[/MATH]が４つ分、[MATH]\(\frac{3}{5}\)[/MATH]は[MATH]\(\frac{1}{5}\)[/MATH]が３つ分と表せます。だから４＋３＝７になります。この７は、[MATH]\(\frac{1}{5}\)[/MATH]が７つあることを表しています。なので、[MATH]\(\frac{7}{5}\)[/MATH]になります。

なるほど。だから[MATH]\(\frac{7}{5}\)[/MATH]になるのか。

答えは[MATH]\(\frac{7}{5}\)[/MATH]になりますね。３つの考え方を見比べて、似ているところはありますか。

すべて、[MATH]\(\frac{1}{5}\)[/MATH]を基にして、いくつ分あるのか考えていると思います。

そうですね。すべての考えが[MATH]\(\frac{1}{5}\)[/MATH]を基にして、いくつ分あるのか考えていますね。つまりＣ１とＣ２の考え方は、Ｃ３のことを表しているんですね。

Ｃ３のことを図や表にして表すと、Ｃ１やＣ２のようになるんだ。

ほかと似ているところはありますか。

何かを基にして計算することは、小数のときにもやったと思います。

なぜ、同じだと思いましたか。

小数のときには0.1を基にして、整数＋整数の考えで計算をしていました。

確かに同じだ。40＋30の計算のときにも、10を基にしていくつ分あるかで計算をしていたね。

そうですね。分母の数に着目して、基となる分数を見付ければ整数のたし算のときと同じように分数＋分数の計算ができそうですね。ほかにできそうなことはありますか。

ほかの分母の数になってもできると思います。

では、[MATH]\(\frac{8}{7}\)[/MATH]＋[MATH]\(\frac{5}{7}\)[/MATH]の計算はできますか。

さっきと同じように考えればできます。

図や表に表して考えますか。

いいえ。基になる分数を見付ければ、整数のたし算のときと同じようにできます。

[MATH]\(\frac{8}{7}\)[/MATH]＋[MATH]\(\frac{5}{7}\)[/MATH]の場合は、基になる分数はいくつですか。

[MATH]\(\frac{1}{7}\)[/MATH]です。

なので、８＋５＝13だから[MATH]\(\frac{13}{7}\)[/MATH]になります。

ほかにできそうなことはありますか。

分数ー分数のときも、今回の分数＋分数と同じように考えればできると思います。

帯分数のたし算もできると思います。

分母の数を見て、同じだったら基になる分数を見付ければ考えられると思います。

そうですね、これからは分数のたし算やひき算は、同じ分母のときには分母の数に注目して、基になる分数を見付け、整数のたし算やひき算と同じようにできそうですね。

できそうです。

これからは、分母の数に注目して分数のたし算やひき算を見ていきましょう。

[MATH]\(\frac{1}{〇}\)[/MATH]を基にすれば、整数のときと同じように計算の仕方を考えることができる。

評価問題

[MATH]\(\frac{7}{5}\)[/MATH]－[MATH]\(\frac{3}{5}\)[/MATH]の計算のしかたを考えよう。

子供に期待する解答の具体例

さっきやった分数＋分数のときのように、[MATH]\(\frac{1}{5}\)[/MATH]を基にして計算の仕方を考えました。[MATH]\(\frac{7}{5}\)[/MATH]は[MATH]\(\frac{1}{5}\)[/MATH]が７つ、[MATH]\(\frac{3}{5}\)[/MATH]は[MATH]\(\frac{1}{5}\)[/MATH]が３つ。なので７－３＝４。この４は[MATH]\(\frac{1}{5}\)[/MATH]が４つあることを表しているので答えは[MATH]\(\frac{4}{5}\)[/MATH]。