小2算数「式と計算」指導アイデア《括弧を使った式に表す/式の考えを読み取る》
執筆/上尾市立瓦葺小学校教諭・澁谷拓也
監修/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫

目次
単元の展開
第1時 3口の加法計算のしかたや( )の使い方が分かる。
▼
第2時(本時)( )を使った式に表したり、( )を使った式から考えを読み取ったりすることができる。
▼
第3時 >、<、=を使った式の表し方が分かる。
本時のねらい
3口の数の加法計算の場面を、( )を用いた式に表したり、( )を用いた式から考えを読み取ったりすることができる。
評価規準
( )の位置に着目して、3口の数の加法計算の場面を式に表したり、考えを読み取ったりして説明している。
本時の展開
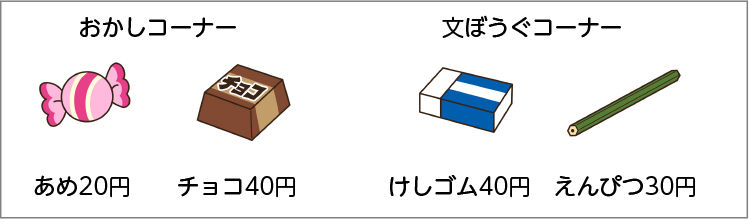
みんなは買い物をしたことがありますか。
あります。
どんなものを買いますか。
鉛筆やお菓子やゲームです。
皆さん、いろいろなものを買いますね。買い物では、いろいろなものを買うとき、金額がいくらになるのかを計算しなければいけません。次のものを一緒に買ったときのことを考えてみましょう。
あめと消しゴムだ。
合わせて買うといくらでしょう。
20+40=60だから、60円です。
今日は買いもので、いくら使ったかを考えてみましょう。

20円のあめと40円のけしゴムを買いました。えんぴつを買いわすれたので店にもどり、30円のえんぴつを買いました。ぜんぶでいくらつかったでしょう。
順番に足せば、答えはすぐ求められます。
20+40=60、60+30=90。答えは90円です。
全部で90円使ったようですね。みんなが考えた式のなかに、こんな2つの式がありました。それぞれの式から、それぞれどのように考えたのかをみんなで考えてみましょう。


( )に着目して、式の意味を考えよう。
見通し
2つの式の違いは、( )の位置だから、足す順序を変えただけなのかな。
( )はひとまとまりの数を表していたから、何が( )でまとめられているのかを考えれば、式の意味が分かるかも。
1つ目は、あめと消しゴムの値段が、2つ目は消しゴムと鉛筆の値段が( )でまとめられているね。
自力解決の様子
A つまずいている子
・( )の意味を捉えず、「3つのものを買ったので、3つのたし算をしている」と説明している。
・( )を先に計算することに注目し、「先に計算するために( )を付けている」と説明している。
B 素朴に解いている子
・C1はあめと消しゴムを先に計算し、C2は消しゴムと鉛筆を先に計算していることを説明している。
・計算の順序に着目して説明しているが、( )を付けた意味までは説明していない。
C ねらい通り解いている子
・計算の順序だけではなく、C1は先に買ったものをまとめて考え、C2は文房具でまとめて計算していることを理解し、説明することができている。
学び合いの計画
自力解決の場面では机間指導を行い、個別的に支援を講じます。
特に、式の意味をうまく言葉で説明できず、手が止まってしまっている子供たちには、「20」「40」「30」の数字が表している意味を考えるように助言します。
また、( )に着目し、数字をまとめて考えていることに気が付いている子供には、前時の学習である( )の意味を生かしていることを評価した後に、( )がどのようなくくりでひとまとまりにしているのかを考えさせることで、式を書いた子供の意図に気付かせます。
さらに練り上げの場面では、式に言葉を書き込んでいる子供や言葉の式で表している子供の考えを取り上げます。
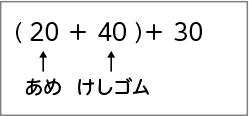
言葉と式を関連させて子供たちに示す活動を繰り返すことで、式には意味があり、言葉で表すことができることへの理解が深まるようにします。
また、まとめているものが、「先に買っているもの」なのか「文房具」なのかによって( )の使い方が変わってくることに着目し、「何を1つのまとまりと考えるか」によって、式での表し方が異なることに気が付くことができるようにします。
ノート例
A つまずいている子
B 素朴に解いている子
全体発表とそれぞれの考えの関連付け
では、どのように考えたか説明してください。
イラスト/横井智美、やひろきよみ



