小3算数「かけ算の筆算1けた」指導アイデア《2位数×1位数の計算》

執筆/目黒区立碑小学校教諭・大村英視
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時 何十、何百×1位数の計算
▼
第2時 被乗数と積の関係の考察
▼
第3時 (本時)2位数×1位数の計算
▼
第4〜7時 2位数×1位数の筆算
▼
第8~9時 3位数×1位数の筆算
▼
第10時 乗法の結合法則
▼
第11時 まとめ
本時のねらい
2位数×1位数の乗法の計算の仕方を考える。
評価規準
2位数×1位数の乗法の計算の仕方を、既習の計算を基に図や式などを用いて考えている。
本時の展開

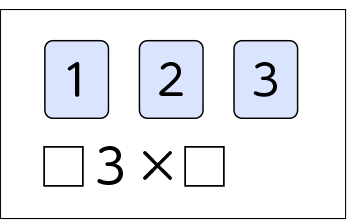
上のように1、2、3の数カードを提示し、はじめは「□3×□」の□にカードを当てはめると、どんな式ができるかを問い、さまざまな式を挙げさせる。すべての子供が場面を理解できたら、答えが一番大きくなる式を問い、子供が自然に答えを見積もる展開とする。
答えが一番大きくなるのは数をどのように入れたときでしょう。
掛ける数が3のときに大きくなりそうだから、23×3です。
掛けられる数の十の位の数が大きいほうが答えも大きくなりそうだから、33×2です。
23×3はおよそいくつになりますか。
23はだいたい20なので、答えは60くらいです。
33×2はどうですか。
33はだいたい30だから、こっちもだいたい60くらいになります。
※答えの見積もりを行い、大きくなりそうな式を2つくらいにしぼる。
それではどちらの計算の答えが大きくなるか計算しましょう。はじめに、23×3の計算の仕方を考えて、答えを求めましょう。

23×3の計算の仕方を考えよう。
自力解決の様子
A つまずいている子
23+23+23=69
累加で答えを求めている。
B 素朴に解いている子
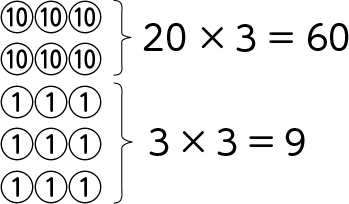
60+9=69
C ねらいどおり解いている子
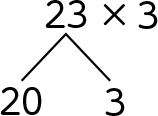
20×3=60
3×3=9
60+9=69
学び合いの計画
自力解決の段階で自分がしていなかった解決方法については、その考えをしていた子供からの説明を聞くのではなく、どのように考えたのか解釈できるように時間を確保します。
図や式を提示して個人で考える時間を短時間確保した後、多くの子供が理解できているようであれば、ペアで考えを共有する時間を設けます。
考え方を理解している子供が少ないようであれば、全体の場で数人の子供にヒントになることを発言させ、それを全体で解釈していきます。
授業支援アプリを活用して、自力解決の内容を端末上で表現させることも可能です。その場合、アレイ図や模擬貨幣の素材を全体で共有しておけば、子供はそれらのイラストを複製することで、計算の仕方を簡単に表現することができます。
全体発表では子供が投稿した画面を提示し、それをほかの子供が説明することで解決方法を共有します。
解決の過程をノートに表現した場合も、授業支援アプリにノートの写真を投稿させることで、互いのノートを共有することができます。
ノート例
イラスト/横井智美

