小3算数「暗算」指導アイデア《100円玉でお買い物|被減数や和が100になる暗算の仕方》
執筆/荒川区立第一日暮里小学校教諭・石川大輔
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時(本時)数の構成に着目して、被減数が100になる暗算や和が100になる暗算による計算の仕方を考える。
▼
第2時 数の構成に着目して、暗算による2位数どうしの加減法の仕方を考え、暗算する。
▼
第3時 2位数どうしの加減法の暗算の仕方を発展的に考察し、習熟する。
本時のねらい
数の構成に着目して、被減数が100になる暗算や和が100になる暗算による計算の仕方を考え、説明することができる。
評価規準
数の構成に着目して、被減数が100になる暗算や和が100になる暗算による計算の仕方を考え、式や図、言葉で説明している。
本時の展開
(お店の図を提示する)ここは、お店です。今、皆さんは100円玉を1枚持っています。

私はチョコレートを買いたい。
僕はグミを買いたいな。
できるだけたくさん買いたいな。
※問題場面を電子黒板で提示する。
先生は89円のジュースを買います。100円玉1枚で払ったとき、おつりは何円になりますか。

89円のジュースを1本買います。
100円玉1まいではらうと、おつりは何円になりますか。
式はどうなりますか
100-89です。
筆算したいな。
今、お店にいるので、紙がありません。100-89を暗算で計算しましょう。
※暗算をさせるために、ワークシートは配らない。鉛筆も筆箱から出させない。

100-89を暗算で計算しよう。
計算できそう。
できるよ。やってみよう。
えぇ、できるかな……。
書いて計算したいなぁ。
おつりを求められた人は立ってください。(おつりを求められた子供は立たせ、実態をつかむ)
※おつりを求められた子供は立ち、おつりを求められなかった子供は座っている。
※30秒程度で時間を区切る。
皆さん、一度座りましょう。座っていた人はどうしたいですか。
筆算したいです。
暗算は難しいよ。筆算ならできるのに。
そうですよね。どのように考えれば暗算しやすいのでしょう。100-89の暗算の仕方を基に考えましょう。
※暗算できる子ではなく、「暗算することが難しい」「書いて計算したい」といったような暗算が難しいと考える子供の思いに共感し、どのように考えれば暗算しやすくなるのかというねらいにつなげる。

どのようにすれば暗算しやすいのか考えよう。
※この段階でワークシートを配る。
見通し
暗算できた人は、頭のなかでどうやって計算したのですか。
まず80円を引いて考えました。
頭のなかで筆算しました。
89円を90円にして考えました。
なるほど。では、それぞれ考えてみましょう。
※見通しでは、暗算の仕方を言葉だけで説明させる。なお、子供が答えを出す過程を詳しく説明し続けた場合は、途中で区切って見通しとする。
自力解決の様子
A つまずいている子
・答えは出せたが、暗算の方法を表現し説明していない。もしくは、計算することができない。
頭のなかだと計算できないな。筆算でやったら、おつりを求められそうなんだけれど……。
B 素朴に解いている子
・数を分けたり何十と見たりして暗算する方法を式や図、言葉などで表現し、説明している。
100-89だから、
まず、100から80を引くと20です。
次に残った20から9を引くと11です。
だから、おつりは11円です。
C ねらいどおり解いている子
・数を分けたり何十と見たりして暗算する方法を式や図、言葉などで構造的に表現し、説明したり、多様に表現し、説明したりしている。
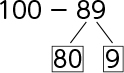
100-80=20
20-9=11
おつり 11円
100-89
89は、だいたい90だから
100-90=10
本当は89だから
多く引きすぎた1を足して
10+1=11
おつり 11円
上記のほかに、次のような考えも出されることが予想されます。
100-89
89はだいたい80だから
100-80=20
まだあと9引くから
20-9=11
おつり 11円
100-89
100を90と10に分けて
90-80=10
10-9=1
10+1=11
おつり 11円
100-89
100を99と見て
99-89=10
足りない1を足して
10+1=11
おつり 11円
100-89
ひき算は、引かれる数と引く数に同じ数を足しても答えは変わらないから
101-90=11
おつり 11円
学び合いの計画
自力解決ではAからCの子供のように答えが求められない子供から根拠をもって多様に考えられる子供が存在します。このような子供らがそれぞれ根拠を明確に持って説明できるように、自力解決では次のように指導します。
Aのような子供には、数を分ける考え方に着目させます。これまでに学習したひき算の計算をふり返らせながら、「まず何-何をする?」といったように計算の手順を問い、分けて計算する考え方を引き出します。場合によっては、筆算による計算を並行させて、暗算の手順を考えさせます。
Bのような子供には「式や図で表しましょう」などと声をかけ、簡潔に説明するように促します。
Cのような子供には、自分が書いた表現や説明を順序よく説明できるように見直させ、場合によっては修正させます。
説明し合う場面では、説明する子供に「暗算の仕方を順序よく説明しましょう」と指示します。手順を明確にさせることで、「分ける」や「何十と見る」という見方が明確になります。
見方・考え方としては、Bのように数を分けて考える子供が多く、何十と見て考える子供は少ない傾向があります。何十と見て考える子供がいない場合は教師が提示し、式や図、言葉から見方・考え方を読み取らせる活動を取り入れます。
全体の話合いでペアやトリオで説明し合う場を設定したり、全体検討である子供が説明したことを再現させたりします。そうすることによって、Aの子供が暗算の仕方を習得できたり、BやCの子供が確かに理解できるようにしたりします。
話合いの後半では「どちらの方法が暗算しやすいですか」と問い、考えやすいほうを自覚させるようにします。
ノート例
イラスト/横井智美、やひろきよみ

