小5算数「割合」指導アイデア
執筆/新潟県公立小学校教諭・新保健介
編集委員/文部科学省教科調査官・笠井健一、新潟県公立小学校校長・間嶋哲
目次
本時のねらいと評価規準(本時の位置 1/12時)
ねらい
シュートのうまさの比べ方について、分かりやすい比べ方を考えることを通して、全体と部分の関係同士で比べる場合があることを理解する。
評価規準
基準量と比較量の関係を式や図・言葉を用いて表し、2つの量を比べることができる。
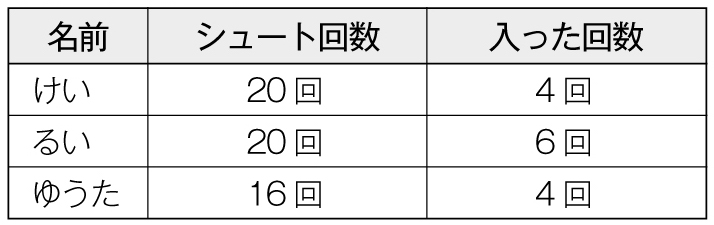
問題場面
バスケットボールの試合で、シュートが一番うまい選手と交代します。どの選手に交代したらいいでしょう。

データを用いてシュートのうまさを比べる方法について問いかけ、発言させながら、差で比べられない場面に気付かせます。
シュートの回数が同じ選手は、すぐに比べられるね。
けい選手とるい選手なら6回入ってるから、るい選手だね。
けい選手とゆうた選手だと、入った回数が同じだから、ゆうた選手だね。
るい選手とゆうた選手は?
シュートの回数も入った回数も違うね。
るい選手の方が失敗が多いね。でも本当にゆうた選手の方がうまいっていえるかな?
るい選手とゆうた選手を比べるとき、どうしたらいいんだろう。
本時の学習のねらい
るい選手とゆうた選手では、シュートがうまいのはどちらだろうか。
自力解決の様子
A つまずいている子
シュート数も入った回数も違うので、失敗数の差で比べている。
B 素朴に解いている子
単位量あたりの大きさの学習を用いて立式し、答えをもとに比べている。
C ねらい通り解いている子
シュートの回数を基準量として1とみて考え、割合を求めて比べている。
学び合いの計画
割合は、差や和で比べられない場面において、2量の関係で比べるために求めます。
イラスト/横井智美
『教育技術 小五小六』 2021年12/1月号より