小5算数「図形の面積」指導アイデア
執筆/新潟県公立小学校教諭・樋浦教之
編集委員/文部科学省教科調査官・笠井健一、新潟県公立小学校校長・間嶋哲
目次
本時のねらいと評価規準(本時の位置 5/12時)
三角形の面積の求め方を、「等積変形」や「倍積変形」の考えを用いて解決し、複数の求積方法の共通点について理解することができる。
評価規準
三角形の面積の求め方を、「求積可能な既習の図形」「2でわる意味」の2つの視点から説明することができる。
問題場面
下の図形の面積を求めよう。

この図形の面積を求めます。どんな図形が隠れているかな?
隠れている図形を子どもたちに予想させる時に、「平行四辺形」という意見を取り上げ、そう考えた意図を聞きます。「Aのところから、横に辺が伸びているかもしれないから」という発言から、この図形を「平行四辺形」と見る(倍積変形)イメージをもたせます。
※本時では、等積変形の他に、倍積変形の考えも引き出したいため。
Aの所から辺が横に伸びれば平行四辺形だけど?
Aの所から、下の方へ辺が伸びていけば、三角形になるよ。どっちの図形かな?
隠れている図形は、三角形でした。三角形の面積を求めることはできるかな?
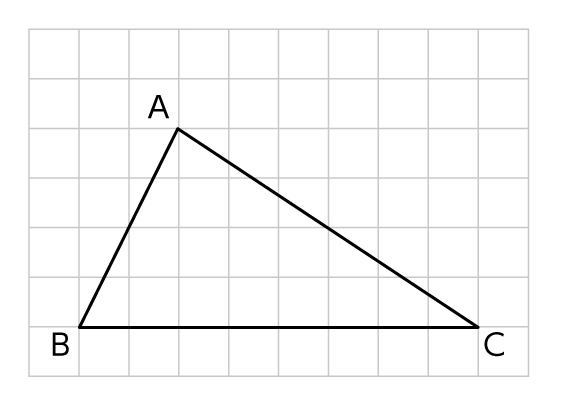
平行四辺形の時みたいに、長方形に直せばいいのかな?
平行四辺形の面積の求め方は勉強したよ。平行四辺形にすることもできるのかな?
本時の学習のねらい
三角形の面積も、面積の求め方を知っている図形に直すと求めることができるかな?
見通し
分けて、その部分を別の所に付けると、平行四辺形や長方形になるよ。
三角形をもう一つ付けると、平行四辺形や長方形になるよ。

見通しをもっている子どもに、分ける場所に直線を引いてもらったり、動かす場所を矢印で示してもらったりします。
自力解決の様子
三角形が書かれたプリントを渡し、「面積を求める方法を1つ見付けたら、他の方法も見付けてみよう」と働き掛けます。渡したプリントは、後でノートに貼るように指示をしておきます。
A つまずいている子
既習の図形に変形できず、面積を求めることができない。
B 素朴に解いている子
「等積変形」で求めることはできたが、「倍積変形」の考え方には気付くことができない。
C ねらい通り解いている子
「等積変形」「倍積変形」どちらの方法でも、面積を求めることができている。
学び合いの計画
自力解決を3分ほど設定した後、3~4人程度のグループを作り、互いの考えや困っていることなどを紹介し合います。
イラスト/横井智美
『教育技術 小五小六』 2021年10/11月号より






