小6算数「場合の数」指導アイデア
執筆／埼玉県公立小学校教諭・山田空
編集委員／文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
（本時3／6時）
ねらい
事象の特徴に着目し、組み合わせ方について、落ちや重なりがないように、図や表を用いて順序よく筋道を立てて考え、調べる。
評価規準
試合の数を求める場面について、落ちや重なりがないように図や表を用いて、組み合わせ方を順序よく筋道を立てて考え、求めることができる。
問題場面
東小学校、西小学校、南小学校、北小学校、各校1チームずつが出場するバスケットボール大会を開きます。どのチームもちがったチームと1回ずつ試合をします。
全部で何試合になるか調べましょう。
どんな組み合わせがありそうですか?
東小対西小、東小対南小、東小対北小、西小対東小などとリレーの並び方を調べた時みたいに、1チームを決めて順々に調べれば簡単だよ。
ちょっと待って、同じ試合があるのはいいのかな。
同じ試合ってどういうこと?
たとえば、「東小学校対西小学校」と、「西小学校対東小学校」は同じ試合だよ。
同じ試合が重ならないように組み合わせを考えないといけないね。今日も落ちや重なりがないように調べたいな。
では、どうすれば落ちや重なりなく試合数を調べられるか考えましょう。
本時の学習課題
落ちや重なりがないように、試合の組み合わせを調べよう。
見通し
まず1チームを決めて、同じ組み合わせがないように重なりに気を付けながら書き出せばいいね。
並べ方を考えた時のように、図を使って調べられそうだ。
球技クラブで使っていた対戦表みたいに、表にまとめられないかな。
自力解決の様子
A つまずいている子
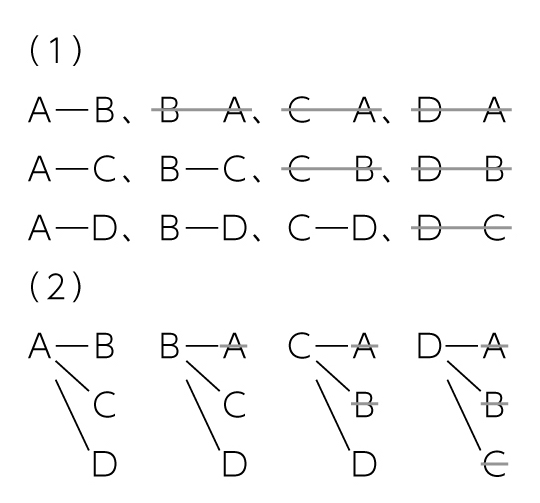
・A―B、C―D、B―C、A―D、A―C、B―D…など、1チームを固定するのではなく、思いつくままに対戦を書き出している。
・A―BとB―Aを別な2通りの事象として捉えている。
B ねらいどおりに解決している子
1チームを固定させながら図や表を用いて順序よく書き出し、重なったものを消している。
C 進んでいる子
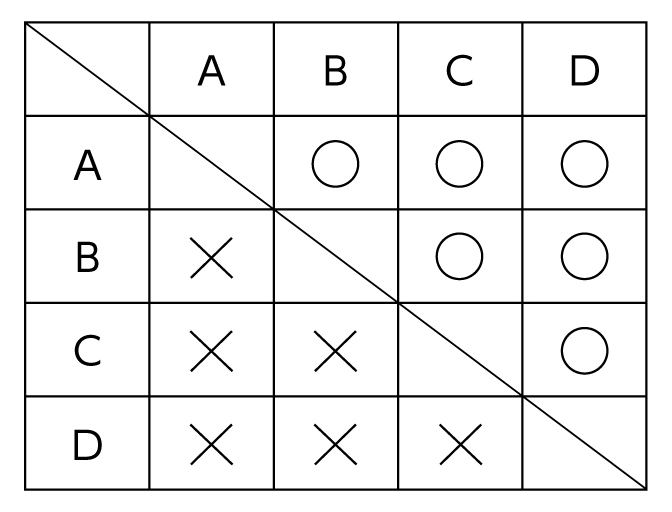
図や表にまとめることにより、落ちや重なりがより分かりやすくなることや、同じ対戦は対角線を挟んで並んでいることに触れながら調べている。
学び合いの計画
イラスト／横井智美
『教育技術 小五小六』2021年10/11月号より
