小4算数「式と計算の順序」指導アイデア《石のまとまりに着目して式の意味を理解しよう》
執筆／福岡県公立小学校教諭・中村翔
編集委員／文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
本時のねらい（本時6／8時）
数のまとまりや演算に着目し、式と場面を結び付けて考える活動を通して、式表現について理解を深める。
評価規準
具体的な場面について式の表す意味を読みとり、説明することができる。（知識・技能）
問題
黒石と白石を合わせた数は何個ですか。
一つの式に書いて求めましょう。
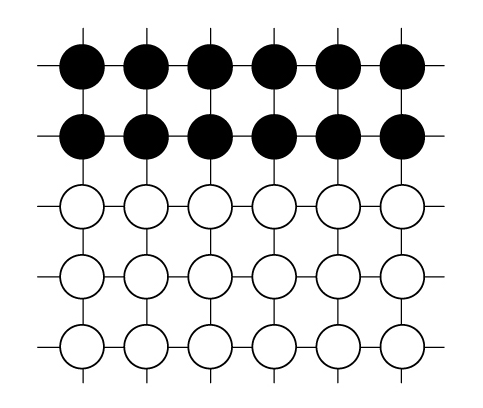
黒石と白石は全部で何個ですか。
5×6＝30だから、30個です。
正解です。式が5×6になることを図で説明してください。
縦に5個、横に6個あるから5×6です。
縦と横の数を逆にして、6×5でもよいと思います。
今日は式と図を結び付けることを考えます。次の3人の考えを図で説明してください。
はなこ：2×6+3×6
しょう：6×2+6×3
たろう：(2+3)×6
学習のねらい
この記事には続きがあります。小学館IDでログインすると最後までご覧いただけます（残り: 1217 文字）
