小4算数「小数のかけ算とわり算」指導アイデア《小数×整数の筆算のしかた》

特集: 【文部科学省教科調査官監修】1人1台端末時代の｢教科指導のヒントとアイデア｣

2022.10.15

単元の展開

第１時　数の構成やかけ算の性質に着目し、小数×1けたの数（0.2×７など）の計算のしかたを考える。
▼
第２時　数の構成やかけ算の性質を基にして、小数×1けたの数（2.3×７など）の立式とその計算の意味について考える。
▼
第３時（本時）前時で学習した小数×1けたの数の計算の意味や整数×整数の筆算のしかたを基にして、小数×1けたの数の筆算（2.3×７など）のしかたについて考える。
▼
第４時　小数×2けたの数の筆算（2.7×12など）のしかたを理解し、その計算ができるようになる。
▼
第５時　小数の範囲を広げて、[MATH]\(\frac{1}{100}\)[/MATH]の計算（2.38×4など）や積に空位のある計算（4.05×36など）の筆算ができるようになる。
▼
第６時　数の構成に着目し、小数÷１けたの数の計算（0.6÷3など）のしかたを考える。
▼
第７時　小数÷１けたの数（7.2÷３など）の立式と、その計算の意味について考える。
▼
第８時　小数÷１けたの数の計算の意味や整数÷整数の筆算のしかたを基にして、小数÷１けたの数の筆算（7.2÷３など、一の位に商あり、あまりなし）のしかたについて考える。
▼
第９時　小数÷１けたの数の範囲を「一の位に商が立たない場合（4.9÷７、4.92÷６など）」に広げて、筆算のしかたを理解し、その計算ができるようになる。
▼
第10時　小数÷２けたの数の筆算（64.8÷36、7.74÷43など）のしかたを理解し、その計算ができるようになる。
▼
第11時　あまりがある場合の小数÷整数の筆算（13.6÷３など）の筆算について考える。
▼
第12時　小数÷整数(15.6÷８など)で割り進みをするときの筆算のしかたを理解し、その計算ができるようになる。
▼
第13時　整数÷整数（２÷３など）で割り進み、割り切れない場合の商の概数処理について理解する。
▼
第14時　小数が何倍かを表すのに用いられることを、倍の計算を基に考える。
▼
第15時　学習内容の定着を確認し、理解を確実にする。

本時のねらい【小数×整数（2.3×７）の立式と計算のしかたについて学習した後】

計算の意味や整数×整数の筆算を基にして、[MATH]\(\frac{1}{10}\)[/MATH]の位までの小数×整数（2.3×７）の筆算のしかたについて考える。

評価規準

小数に整数を掛ける筆算のしかたについて、計算の意味や整数の筆算のしかたなどと関連付けて考えている。（思考･判断･表現）

本時の展開

リボンを１人に2.3ｍずつ配ります。このリボンを７人に配るには、リボンは何ｍいりますか。

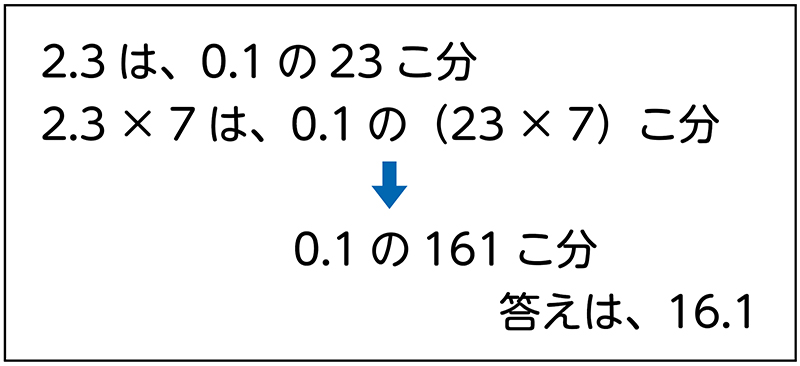
前の時間は、この問題についてみんなで考えて、式は2.3×７になることが分かりました。そして、0.1のいくつ分と見て考えれば、2.3は0.1の23個分だから、2.3×７は0.1の（23×7）個分になるので、23×７＝161で、答えは16.1ｍになるということを考えました。
また、2.3を10倍して23×７の計算をすると161なので、その161を10で割ると答えの16.1が求められるということも考え出しました。

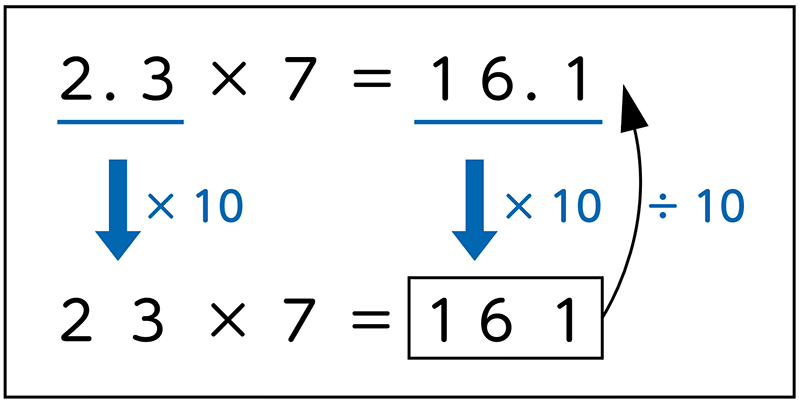
ところで、前の時間に学んだこれらのことを生かして、2.3×７の筆算ではできないでしょうか。

答えが16.1と分かっているので、筆算ができるはずです。

前の時間の学習を基にしたら、筆算はできるのではないかな……。

0.1のいくつ分かと見て考えれば、2.3は0.1が23個分だから、23×７で考えるといいと思います。だから、23×７の筆算が使えると思います。

2.3×７は、23×７に似ています。23×７の筆算ならできるので、掛けられる数の2.3を10倍して計算して、積を10で割る方法を使えば、考えていけそうです。

整数の筆算をうまく使えば、小数の筆算ができると思います。

それでは、整数×整数の筆算のしかたを基にして、小数のかけ算の筆算について考えていきましょう。

整数の筆算を基にして、2.3×７（小数×整数）の筆算のしかたを考えよう。

見通し

0.1がいくつ分かを考えると、計算できそうだよ。（方法の見通し）

小数を10倍して整数に直し筆算すると、計算できそうね。（方法の見通し）

整数で計算した答えと、小数のかけ算の答えを比べて考えよう。（結果の見通し）

自力解決の様子

A つまずいている子

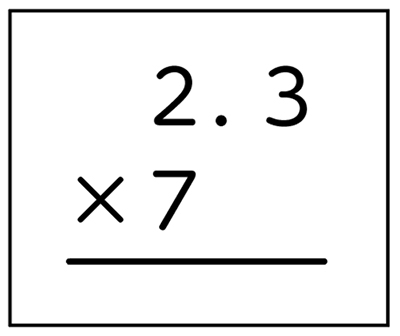
筆算の形式に置くときに、小数のたし算・ひき算の影響から位をそろえて、一の位の２の下に７を書いてうまくいかない。

Ｂ素朴に解いている子

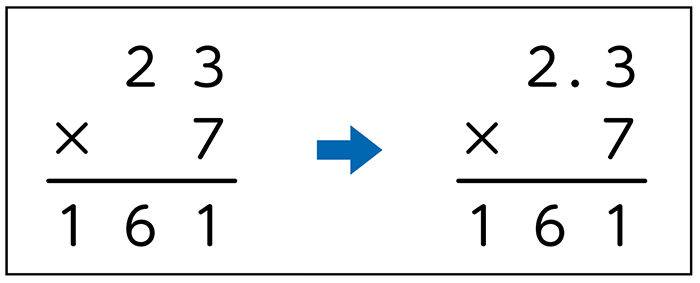
整数の筆算と同じ手順で計算をしている。小数点の扱いにとまどっている。

Ｃねらい通り解いている子

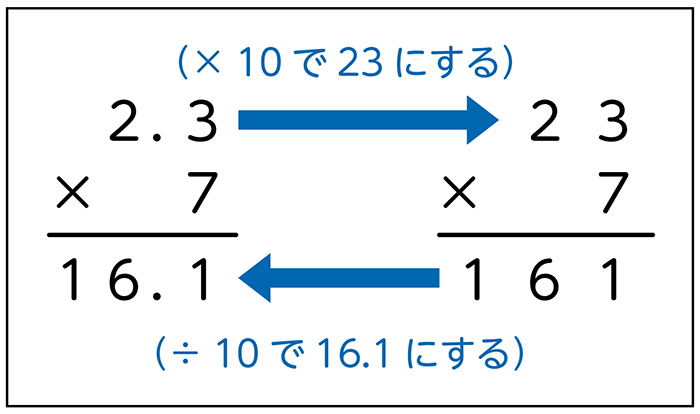
整数の筆算と同じ形式・同じ手順で計算し、数のしくみやかけ算の性質とつなげて、筆算のしかたを考えている。

学び合いの計画

この単元では、既習事項である小数のしくみ（数の構成）や整数のかけ算・わり算の性質を生かして、小数のかけ算・わり算の筆算のしかたを考えていきます。本時では、子供たちが、既習の整数×整数の筆算の方法を基にして、小数×整数（1けた）の筆算をつくり出すことをねらっています。

そのためには、これまでに学んできた小数のしくみや、第４学年で学んだ小数のたし算・ひき算、かけ算のきまり（掛ける数が10倍になると積も10倍になる）などの理解の程度を確認しておきます。

子供たちが自分のもっている力を駆使して、めあてに向けて学んでいく力を育むうえでも、既習の学習を整理していくことは大切です。

指導にあたっては、整数の筆算と小数の筆算の共通点や違いを見付けながら、子供たちがよりよい方法を考えていくようにします。子供たちのつまずきに寄り添ったり、ポイントとなる発言をうまく取り上げたりしながら学びを深めていきましょう。

学習後には、生活のなかから小数を使っている場面をイメージして問題づくりに取り組むと、さらに小数の計算の大切さを実感することにつながるでしょう。

ノート例

全体発表とそれぞれの考えの関連付け

23×７の筆算を基にして、2.3×７の筆算のしかたを考えましょう。

一の位の計算の２×７＝14はできるけど、0.3をどうすればよいか困っています。

かけ算だから、小数のたし算みたいに位をそろえなくてもよいと思うよ。

23×7の筆算とまったく同じように、３の下に掛ける数の７を書いて整数として計算して、あとで積を小数に戻したらいいよ。

2.3を小数のまま書いて計算して、積の161を10で割って小数点を付けて、16.1にします。

この筆算のしかたは、2.3を10倍して計算して、その積を10で割るということと同じだよ。

整数のかけ算の筆算は位ごとのかけ算を合わせた仕組みになっています。だから、掛けられる数が小数になっても位ごとのかけ算をしていけるはずです。

確かに、最初の３×７の計算は、0.3×７＝2.1を計算しているということだよね。[MATH]\(\frac{1}{10}\)[/MATH]の位の計算だね。その後の、２×７＝14は、一の位の計算をしているということだね。

整数も小数も、それぞれの位が０〜９で、10になると上の位に移るという数のつくり方が同じだから、整数の筆算のしかたと小数の筆算のしかたが同じなんだね。

なるほど、小数が整数と同じ数の仕組みでできているから、整数でできる筆算のしかたが小数でも使えるというわけね。

１人１台端末活用ポイント

整数×整数の筆算と、小数×整数の筆算を書いたものを全員に配付し、パソコン上に手書きで考えを書き入れます。それを見合うことで、整数×整数の筆算から、小数×整数の筆算へとつなぐための共通点や違いが見えてくると思います。

全体に広めたい考えを共有できれば、大切なことが伝わります。また、教科書に付属のデジタルコンテンツをうまく利用して、小数点を意識し、筆算をする方法を見ることができるものもあります。それぞれのコンテンツの特徴をうまく活用しましょう。

2.3×７の筆算は、23×7の筆算と同じしかたでできる。
①小数点を考えずに、右にそろえて書く。

×10をして、2.3を23にするということ。
②整数のときと同じように計算する（３×７＝21、２×７＝14）。

③掛けられる数の小数点にそろえて積の小数点を打つ。

÷10をして、161を16.1にするということ。

小数×整数の筆算は、整数×整数の筆算と同じしかたでできる。