小3算数「分数」指導アイデア《分割分数と量分数の違い》
執筆/神奈川県横浜市立嶮山小学校教諭・梅本樹徳
監修/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥

目次
単元の展開
第1時 1mを等分してできる大きさの分数による表し方
▼
第2時 単位分数を用いた分数の表し方
▼
第3時 分数・分母・分子の意味、端数部分の大きさの分数による表し方
▼
第4時 分数を数直線上に並べ、分数を整数と同様の数として捉える。
▼
第5時 1より大きい分数の表し方
▼
第6時(本時)分割分数と量分数の違いについて理解
▼
第7時 0.1を単位とした小数と[MATH]\(\frac{1}{10}\)[/MATH]を単位にした分数の大きさの関係
▼
第8時 同分母の分数の加法・減法の計算
本時のねらい
[MATH]\(\frac{3}{4}\)[/MATH]mと基準量の[MATH]\(\frac{3}{4}\)[/MATH]の違いを見いだし、量分数と分割分数の違いを捉えることができる。
評価規準
基準量に着目し、単位分数の大きさを明らかにして、分数の大きさを表現する方法を考えている。
本時の展開
Aのテープ(黄色い部分)の長さは何mでしょうか。
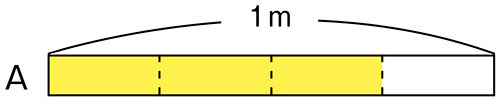
[MATH]\(\frac{3}{4}\)[/MATH]mです。
どうしてそう言えるのですか。
1mを4等分した三つ分だからです。
[MATH]\(\frac{1}{4}\)[/MATH]mが三つ分になるからです。
では、Bのテープ(黄色い部分)の長さは何mでしょうか。

2mの[MATH]\(\frac{3}{4}\)[/MATH]だから、[MATH]\(\frac{3}{4}\)[/MATH]mだと思います。
でも、Aの長さと同じになってしまうよ。
分数だからいいんじゃないかな。
長さが違うのに、どちらも[MATH]\(\frac{3}{4}\)[/MATH]mと言っていいのかな。
Bのほうは何mと言えるのか、ちゃんと調べないといけないな。

基準量に着目し、分割分数と量分数の違いについて説明することができる。
見通し
1mよりも長いのだから、[MATH]\(\frac{3}{4}\)[/MATH]mではおかしい。(結果の見通し)
長さを分数で表すには、1mを基にして考えてきたよ。(解決の見通し)
AやBのテープの1mを基にして、1つ分がいくつになるかを調べればいい。(解決の見通し)
自力解決の様子
A つまずいている子
基準量に当たる1mに着目できない。単位分数がいくつになるかが見いだせない。
B 素朴に解いている子
Bのテープの1mに着目し、[MATH]\(\frac{1}{2}\)[/MATH]mがいくつ分かを考えている。
C ねらい通り解いている子
Bだけでなく、Aのテープの[MATH]\(\frac{1}{4}\)[/MATH]mを使って、Bの長さが表せないかを考えようとしている。
学び合いの計画
1mの[MATH]\(\frac{3}{4}\)[/MATH]と2mの[MATH]\(\frac{3}{4}\)[/MATH]では、長さが明らかに異なるにもかかわらず、子供たちはどちらも[MATH]\(\frac{3}{4}\)[/MATH]mと捉えてしまう傾向があります。
イラスト/横井智美

