小6算数「円の面積」指導アイデア《複合図形を分割して面積を求めよう》
執筆/埼玉県公立小学校教諭・関裕也
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
(本時4/6時)
ねらい
円を含む複合図形の面積について、既習の求積可能な図形の面積を基にして分割して考え、図や式を用いて説明することができる。(思考力、判断力、表現力等)
評価規準
既習の求積可能な図形を基にして、図や式を用いて説明することができる。
問題場面
下の図で、色をぬった部分の面積を求めましょう。
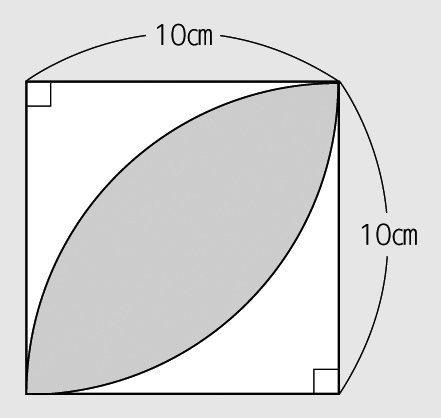
前時までに、円や半分の円、[MATH]\(\frac{1}{4}\)[/MATH]の円の面積を求めることができるようになりました。
この図形の面積を求めることができるでしょうか。
正方形の中に葉のような形があるけれど……。
正方形の一辺を半径とする[MATH]\(\frac{1}{4}\)[/MATH]の円が重なっている図形だね。
重なりの部分を求める公式ってあるのかな?
線を引いて求められる形にして計算したらどうかな。
どのように工夫したら求められるか考えましょう。
本時の学習課題
どのように考えたら、複雑な図形の面積を求めることができるだろう。
見通し
[MATH]\(\frac{1}{4}\)[/MATH]の円と正方形の面積を使って考えてみよう。
[MATH]\(\frac{1}{4}\)[/MATH]の円から直角三角形の面積を引いて考えてみよう。
正方形から[MATH]\(\frac{1}{4}\)[/MATH]の円の面積を引いて求められないかな。
自力解決の様子
A つまずいている子
[MATH]\(\frac{1}{4}\)[/MATH]の円が2つあり、面積も求められるが、その先がどうしたらよいか分からない。
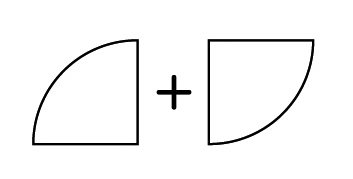
B [MATH]\(\frac{1}{4}\)[/MATH]の円と直角三角形を基に考える子
10×10×3.14÷4=78.5
10×10÷2=50
78.5-50=28.5
28.5×2=57 57㎠
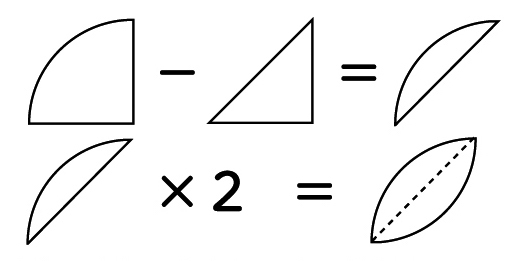
C 正方形から[MATH]\(\frac{1}{4}\)[/MATH]の円の面積を引いて考える子
10×10=100
10×10×3.14÷4=78.5
100-78.5=21.5
21.5×2=43
100-43=57 57㎠
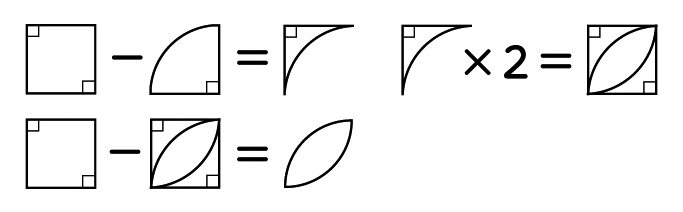
学び合いの計画
複合図形は、既習の図形がどのように組み合わされているのか、見方を変えて考える必要があります。既習の図形にはどのようなものがあったのかを振り返らせ、今回の複合図形の中に見える既習の求積可能な図形を捉えられるようにします。
イラスト/横井智美
『教育技術 小五小六』2021年8/9月号より

