小5算数「分数のたし算とひき算」指導アイデア《異分母分数の通分を理解しよう》
執筆/新潟県公立小学校教諭・濱中大輝
編集委員/文部科学省教科調査官・笠井健一、新潟県公立小学校校長・間嶋哲
目次
本時のねらいと評価規準(本時の位置 5/10時)
ねらい
異分母分数について、図と通分を関連づけていくことを通して、分母を揃えれば計算できることを理解することができる。
評価規準
異分母分数について、分母を揃えると計算できる理由を説明することができる。
問題
2つの入れ物に、[MATH]\(\frac{1}{3}\)[/MATH]Lと[MATH]\(\frac{1}{2}\)[/MATH]L のジュースが入っています。合わせて何L ありますか?
「[MATH]\(\frac{1}{3}\)[/MATH]Lと」まで提示した後に間を取り、問題の続きを考えさせる。ここで既習の同分母分数を想起させることで本時との違いを比較できる素地をつくる。
この(「[MATH]\(\frac{1}{3}\)[/MATH]Lと」まで板書した)後は、どうなると思いますか?
[MATH]\(\frac{1}{3}\)[/MATH]とかならいいのに。
でも、今回は分母が違うんじゃないかな。
(問題文の続きを書く。)今までの学習と違うところはありますか?
今日は、分母が違うたし算になってる。[MATH]\(\frac{1}{3}\)[/MATH]+[MATH]\(\frac{1}{2}\)[/MATH]だよね。
どこをたしたらいいかわからないよ。
本時の学習のねらい
分母がちがうたし算は、どのように計算すればよいか。
見通し
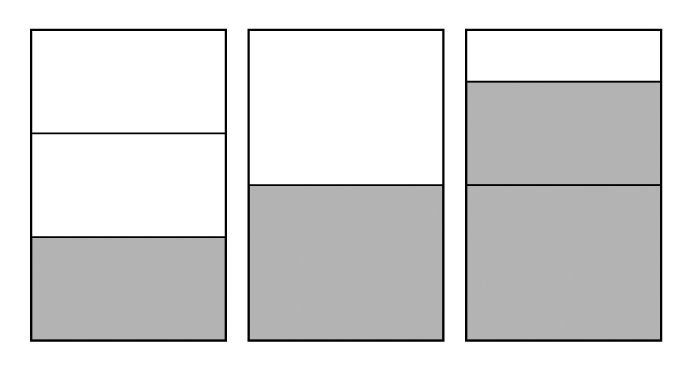
[MATH]\(\frac{1}{3}\)[/MATH]Lと[MATH]\(\frac{1}{2}\)[/MATH]Lを図に書いてみると、合わせたときどれくらいの量になりそうですか?
あともうちょっとで1Lになりそう!
大体の量はわかるけれど、めもりの幅が違うからわかりにくい。
分母が違うとめもりの幅が揃ってないからうまく数えられない。
分母がどうなったら計算できたり、数えられたりしそう?
分母が同じになったら計算できる。
[MATH]\(\frac{1}{3}\)[/MATH]+[MATH]\(\frac{1}{2}\)[/MATH]のやり方を図や計算で考えましょう。
自力解決の様子
A つまずいている子
・分母と分子をたしている。
[MATH]\(\frac{1}{3}\)[/MATH]+[MATH]\(\frac{1}{2}\)[/MATH]=[MATH]\(\frac{2}{5}\)[/MATH]
・大きい分母に合わせている。図から解釈している。
[MATH]\(\frac{1}{3}\)[/MATH]+[MATH]\(\frac{1}{2}\)[/MATH]=[MATH]\(\frac{2}{3}\)[/MATH]
B 素朴に解いている子
通分して分母を6に揃えて計算している。
[MATH]\(\frac{1}{3}\)[/MATH]+[MATH]\(\frac{1}{2}\)[/MATH]=[MATH]\(\frac{2}{6}\)[/MATH]+[MATH]\(\frac{3}{6}\)[/MATH]=[MATH]\(\frac{5}{6}\)[/MATH]
C ねらい通り解いている子
通分し、計算したことを図でも解釈できている。
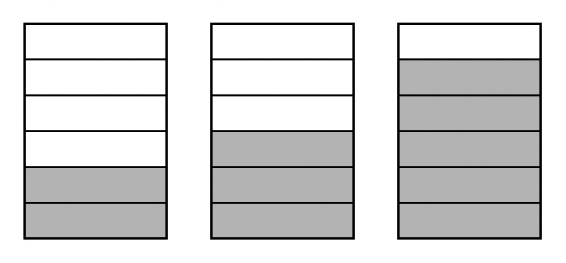
学び合いの計画
イラスト/横井智美
『教育技術 小五小六』 2021年8/9月号より

