小4算数「そろばん」指導アイデア《そろばんによる簡単な小数のたし算》
執筆／富山県射水市立大島小学校教諭・前田正秀
監修／文部科学省教科調査官・笠井健一、前・富山県南砺市立福光東部小学校校長・中川愼一
目次
単元の展開
第１時（本時）そろばんによる簡単な小数のたし算（2.73＋1.84など）、そろばんの特徴
▼
第２時 そろばんによる簡単な小数のひき算（1.25－0.76など）
▼
第３時 そろばんによる大きい数のたし算とひき算（31億＋28億、89兆－63兆など）
本時のねらい
そろばんを用いた小数のたし算について、十進位取り記数法の仕組みと関連付けながら、計算のしかたを考える。
評価規準
そろばんの仕組みに着目し、十進位取り記数法の仕組みと関連付けながら、小数のたし算のしかたを考えている。（思考･判断･表現）
本時の展開
２.７３＋１.８４
2.73＋1.84を計算します。まずは、筆算で計算してみましょう。
筆算したら、4.57になりました。
次は、そろばんで計算してみましょう。最初に、2.73を入れましょう。どんな操作をしたか、説明しましょう。
２は、一の位の桁に、一玉を二つ入れました。
定位点のあるところが一の位です。
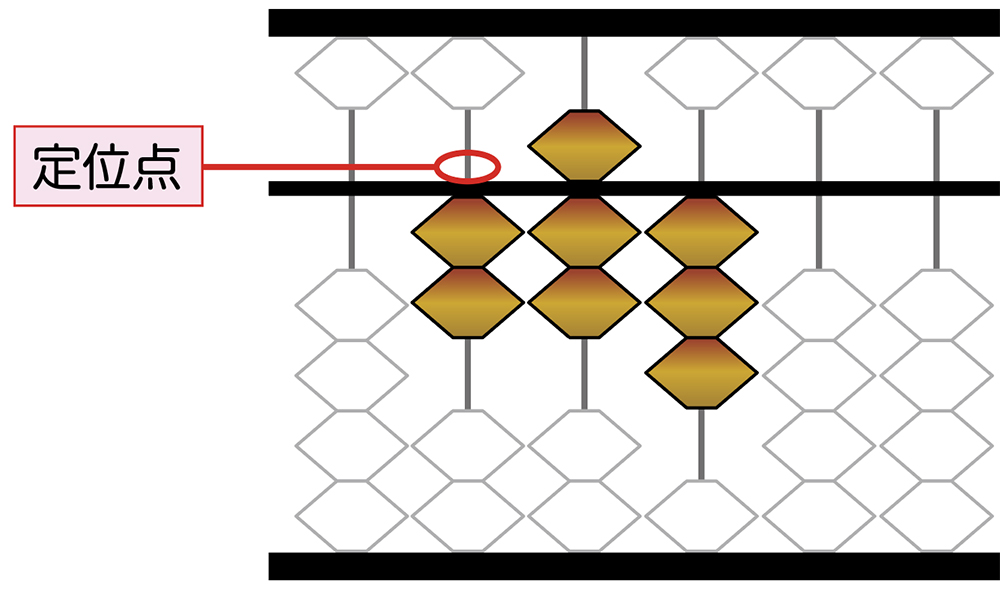
定位点と小数点を勘違いしそうですが、一の位ですね。
７は、[MATH]\(\frac{1}{10}\)[/MATH]の位に、五玉を一つと一玉を二つ入れました。
[MATH]\(\frac{1}{10}\)[/MATH]の位は、定位点の右です。
３は、[MATH]\(\frac{1}{100}\)[/MATH]の位に、一玉を三つ入れました。
そこに、1.84を足します。そろばんは、大きい数から計算します。まずは、１を足しまょう。
一の位に１を足しました。
次に0.8を足しましょう。
あれ、足したいけど、玉が８つないよ。どうすればいいんだろう。
玉が足りないので、２を引いて10を入れます。0.1の位から２を引いて、１の位に１を足しましょう。
８はあと２で10になる数だから、2を引いておいてから10を足すんですね。
今の場合は、0.2を引いておいてから１を足すということですね。
次は、0.04を足します。
あれ、足したいけど、玉が４つないよ。どうすればいいんだろう……。
さっきみたいに、6を引いて10を足せば……、あれ、できないよ。
筆算ならできるのに……。
３＋４は７と分かっているけど、そろばんのやり方って、ちょっと違っているみたいね……。
どうすれば0.03に0.04を足すことができるのかを考えながら、そろばんを用いた小数の計算のしかたを考えていきましょう。そして、筆算と比べて、そろばんを使った計算の特徴やよさを明らかにしていきましょう。
0.03＋0.04について考えて、そろばんを使った計算の特徴やよさを明らかにしよう。
見通し
- 計算方法の見通し
「0.03＋0.04」を考えるには、「３＋４」を考えればよい。（方法の見通し）
五玉を使えば、できそう。（方法の見通し）
「８」を「10－２」と見たように、「４」を「５－１」と見ればよい。（結果の見通し）
- そろばんのよさについての見通し
そろばんが位ごとに計算するのは、筆算に似ている。
そろばんが上の位から計算するのは、暗算に似ている。
自力解決の様子
A つまずいている子
- 0.03＋0.04が0.07だということは分かるが、そろばんの操作のしかたについてはおぼつかない。
- そろばんは、筆算よりも面倒な道具だと考えている。
Ｂ 素朴に解いている子
- 「３＋４＝７」であることから、五玉を入れて「５」にして、３つの一玉の一つをはらって「２」にして、「７」をつくっている。
- そろばんは筆算の代わりになる道具として、その特徴を考えている。
Ｃ ねらい通り解いている子
- 「４」を「５－１」と見て、一玉の一つをはらって、五玉を入れている。
- そろばんによる計算のしかたを理解し、筆算と比べて、その特徴を考えてる。
学び合いの計画
「そろばん」の学習は、「そろばんを学ぶ」というより、「そろばんで学ぶ」と捉えたほうが授業をしやすいでしょう。そろばんを通して、十進位取り記数法の原理についての理解を深めていくイメージです。そろばんも筆算も十進位取り記数法の原理に基づいているということは同じです。
イラスト／横井智美
-
小４理科「季節と生物（冬と春のおとずれ）」指導アイデア
-
小６理科「土地のつくりと変化」指導アイデア
-
小５算数「速さ」指導アイデア《速さと道のりから時間を求める》
-
小６算数「比と比の利用」指導アイデア《等しい比の性質を使い、同じ濃さの乳酸飲料の量を考える》
-
小６算数「拡大図・縮図」指導アイデア《１つの頂点を中心とした拡大図・縮図のかき方》
-
小５算数「図形の角」指導アイデア《図形の角の大きさに着目し、三角形の内角の和について発展的に考える》
-
小５算数「整数の性質」指導アイデア《約数、公約数、最大公約数の意味の理解》
-
小２国語科「かたかなで書くことば」全時間の板書＆指導アイデア
-
小６体育「ベースボール型【ボール運動】」指導アイデア
-
小５体育「マット運動【器械運動】」指導アイデア
