小5算数「速さ」指導アイデア《速さの比べ方》

特集: 【文部科学省教科調査官監修】１人１台端末時代の教科指導ヒントとアイデア

2022.06.17

単元の展開

第１時（本時）速さの比べ方について考える。
▼
第２時　単位量あたりの大きさを用いて、速さを比べる方法について考える。
▼
第３時　速さと時間から道のりを求める方法について理解する。
▼
第４時　道のりと速さから時間を求める方法について理解する。
▼
第５時　速さについてのいろいろな問題を考える。

本時のねらい

時間と道のりという二つの数量の関係に着目し、単位量あたりの大きさを用いて、速さを比べる方法について考える。

評価規準

１時間あたりに進む道のりや１mあたりに進むのにかかる時間を求め、速さを比べる方法を説明することができる。（思考・判断・表現）

本時の展開

どちらが速いと言えるでしょうか。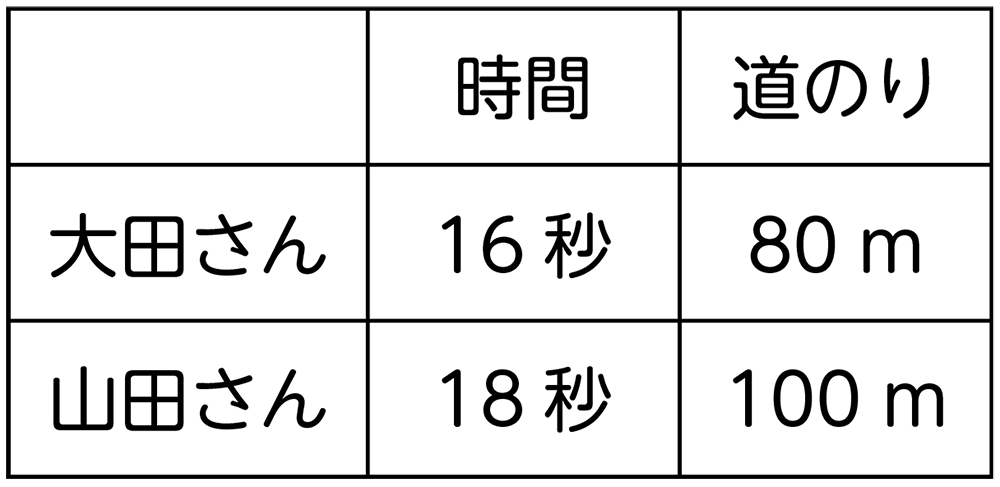

※最初は時間だけを提示し、速さを比べるためには時間だけではなく、道のりも必要であることに気付かせるとよいでしょう。

大田さんは16秒で80ｍ走っています。時間が半分の８秒だとなんｍ走れそうですか。

40ｍだと思います。

40ｍとは言えないと思います。最初の８秒はスピードが出てないから、40ｍ進まないかもしれません。

最初はスピードが出ていて、後半のほうが遅くなるかもしれません。だから40ｍより進んでいるかもしれません。

確かに、実際に走ってみると、ずっと同じ速さで走っているわけではないですよね。だとすると、２人の速さを比べることはできないのでしょうか。（散らばりの様子が違う、混み具合の図を提示しながら）前に、混み具合を比べたときに、どのように考えましたか。

混み具合の学習のときは、ならして考えました。

時間と道のりの場合は、どのように考えたらよいでしょう。

大田さんも山田さんも実際は速かったり、遅かったりするけれど、ならして「同じ速さで進む」というように考えればよいと思います。

時間と道のりが比例すると考えるとよいと思います。

なるほど。「混み具合」を比べるときと同じように、ならして考えたり、比例と考えたりすることが大切ですね。それでは、時間と道のりが比例しているとすると、大田さんが８秒走るとなんｍ走れそうですか。

８秒は16秒の半分だから、同じ速さだったら半分の40ｍ走れると思います。

これからは大田さんも山田さんも、時間と道のりが比例すると考えることにしましょう。どちらが速いかどのようにして比べますか。

時間か道のりがそろっていれば比べられると思います。

どのようにしてそろえたらよいでしょう。

１秒でどれだけ進んだか分かれば比べられると思います。

時間と道のりが比例しているから、数直線で考えるとよいと思います。

では、数直線を使って、１秒でどれだけ進むか、比べてみましょう。

「１秒あたりに進む道のり」で、２人の速さを比べよう。
※導入のやりとりでは、速さを比べるために、時間と道のりという二つの量に着目する必要があることと、「速さの均一性」を話題にしながら、問題場面のイメージを豊かにすることが大切です。「混み具合」の学習を想起させながら、「等しい速さで走り続けると見なす」ことの共通理解を図ります。

見通し

【考え方】
・1秒でどれだけ進むか比べる。
・「同じ速さ」で進むと考える。
【方法】
・数直線

自力解決の様子

A つまずいている子

問題場面を数直線で表すことができない。

Ｂ図を使って解いている子

問題場面を数直線で表すなどして、１秒あたりに進む道のりを求め、正しい結論を導いている。

Ｃねらい通り解いている子

１秒あたりに進む道のりと１ｍあたりにかかる時間を求め、正しい結論を導いている。

Ａの子供に対しては、大田さんの場合について、まず数直線上に16秒と80ｍを位置付けた後、８秒だと40ｍ進むことを書かせるなど、比例のイメージをもたせながら、１秒間に進む道のりを考えさせます。１秒と16秒が16倍の関係になっていることから、２本の数直線に「矢印」と「×16」、さらには「逆方向の矢印」と「÷16」を順に書かせるなどして、数量の関係を把握させていきます。

ＢやＣの子供についても自力解決の際に、「１ｍあたりにかかる時間」と「１秒あたりの道のり」の意味を理解して解決しているかを注意深く見とることが大切です。わり算を立式していても、「とりあえずわり算をしてみる」ことにとどまっている可能性もあります。

式だけを書いている子供には、1秒あたりに進む道のりが80÷16で求めることができるわけについて、数直線を用いて考え、説明させる活動を取り入れるとよいでしょう。

学び合いの計画

タブレットで友達の考えを共有できるICT環境が整備されている場合、自力解決の段階でノートに自分の考えをつくった子供に、その考えをタブレットで画像として保存し、提出させることで、クラス全体で共有することも考えられます。例えば、Ｂの子供が１ｍあたりの解法に触れることができます。

ただし、他人が書いた完成された図を理解することは必ずしも容易でありません。集団の学習ではできあがった図ではなく、数直線上に数値を徐々にかき込みながら説明させ、理解させていくという指導が大切です。

まず、大田さんの１秒あたりに進む道のりについて、素朴に解いた子供に、数直線をかくところまで発表させます。

では、大田さんの速さについて、どのような数直線をかいたか、黒板にかいてみてください。

（下のような数直線をかく。このとき、かく順序も説明させる）大田さんは16秒で80ｍ走っています。１秒あたりに進む道のりを求めたいので、□にします。時間と速さは比例しているから、どちらも×16になっています。

大田さんの数直線をかいていない人は、ノートにかきましょう。同じように山田さんの数直線をかいてみましょう。数直線がかけたら、隣の友達どうしで１秒で進む道のりを求める式と答えを相談して、どちらが速いか考えていきましょう。

ノート例

Ａつまずいている子

Ｂ素朴に解いている子

全体発表とそれぞれの考えの関連付け

全体発表では、数直線を基に1秒あたりに進む道のりを式で求める方法を押さえます。また、1ｍ進むのにかかる時間で速さを比べることができることも確認します。

このとき、1秒あたりに進む道のりでは商が大きい場合が速く、１ｍあたりにかかる時間では商が小さいほうが速いことを日常生活の速さ比べと関連付けるなどとして、確実に理解させましょう。

「80÷16」という計算をしている人がいますね。この計算で何を求めているのでしょうか。数直線を使って説明できますか。

さっき書いた数直線から、□に16をかけると80になることが分かります。□を求める計算は80÷16で５です。1秒あたりに進む道のりは80÷16で５ｍです（同様に山田さんの1秒あたりに進む道のりが100÷18＝5.5……ｍであることを確認する）。

どちらのほうが速いと言えますか。

山田さんです。

「80÷16」ではなく、「16÷80」を計算した人もいますね（計算した子供に説明させる）。

この数直線では、１ｍ進むのにかかる時間を求めています。大田さんは80ｍを16秒で走っているので、１ｍあたりの時間を求めるためには、□×80＝16という式から、16÷80＝0.2秒となります。

１ｍ進むのに0.2秒かかるんですね。山田さんの速さはどのようになりましたか。

山田さんは100ｍを18秒で走っているので、１ｍあたりにかかる時間を求めるためには、□×100＝18という式から、18÷100＝0.18。1ｍあたり0.18秒となります。

どちらが速いと言えますか。

大田さんは１ｍ進むのに0.2秒、山田さんは１ｍ進むのに0.18秒かかるから、山田さんのほうが速いと言えます。

山田さんの0.18のほうが数が小さいのに、速いと言えるのはどうしてですか。

どちらも１ｍ走るのにかかる時間だから、時間が短いほうが速いと思います。

50ｍ走でも、かかった時間が少ないほうが速いです。

速さを比べるときも、混み具合を比べるときと同じように、「単位量あたりの考え」を使うことができる。

評価問題

二つの車のうち、速いと言えるのはどちらですか。

本時の評価規準を達成した子供の具体の姿

「１秒あたりの道のり」と「１ｍあたりにかかる時間」を数直線を使うなどして、正しく立式し、Ａ車のほうが速いという判断ができている。

感想例

・混み具合と速さが同じ考えでつながっていたので、びっくりした。
・実際には速さは一定ではないけれど、１あたりの考えでは一定だと考えて計算するというところがなるほどと思いました。
・数直線を使うと、正しい式を間違えずにつくることができる。

イラスト／横井智美

小学館IDをお持ちの方はこちら

初めてご利用の方