小2算数「大きい数のたし算とひき算」指導アイデア(6/10時)《3位数-2位数の筆算》
執筆/東京都目黒区立駒場小学校主任教諭・越後真紀
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時 2位数+2位数=3位数(百の位への繰り上がりあり)の筆算のしかたを理解し、その計算ができる。
▼
第2時 2位数+2位数=3位数(十、百の位への繰り上がりあり)や2位数+1・2位数=3位数(百の位への波及的繰り上がりあり)の筆算のしかたを、数の見方や既習の加法筆算のしかたを基に考え、説明することができる。
▼
第3時 学習内容を適用して、問題を解決する。
▼
第4時 3位数-2位数(百の位からの繰り下がりあり)の筆算のしかたを理解し、その計算ができる。
▼
第5時 3位数-2位数(十、百の位からの繰り下がりあり)の筆算のしかたを基に考え、説明することができる。
▼
第6時(本時) 3位数-1・2位数(十、百の位からの波及的繰り下がりあり)の筆算のしかたを理解し、その計算ができる。
▼
第7時 3位数-1・2位数(十、百の位からの波及的繰り下がりあり)の筆算のしかたを理解し、その計算ができる。
▼
第8時 3位数+1・2位数(百の位への繰り上がりなし)や3位数-1・2位数(百の位からの繰り下がりなし)の筆算のしかたを理解し、その計算ができる。
▼
第9時 3位数+1・2位数(百の位への繰り上がりあり)や3位数-1・2位数(百の位からの繰り下がりあり)の筆算のしかたを理解し、その計算ができる。
▼
第10時 学習内容の定着を確認するとともに、数学的な見方・考え方をふり返り、価値付ける。
本時のねらい
3位数-1・2位数(百の位からの波及的繰り下がりあり)の筆算のしかたを理解し、その計算ができる。
評価規準
波及的繰り下がりについて、筆算のしかたを操作や図、式を用いて説明している。
本時の展開
64円のポテトチップスを買いたいと思います。お財布の中を見たら、102円ありました。ポテトチップスは買えそうですか。
買えます。
残りのお金は、いくらぐらいになると思いますか。
40円ぐらいだと思います。
102-64で計算できます。
なんだか、大きい数で計算が難しそうですね。
そういうときは、筆算で計算すればいいと思います。
なるほど、前の時間までに、3桁-2桁の計算は、筆算にすれば簡単に計算することができましたね。では、今回も筆算でやってみましょう。

102-64をひっ算でしよう。
前より、数が小さいから簡単だ。
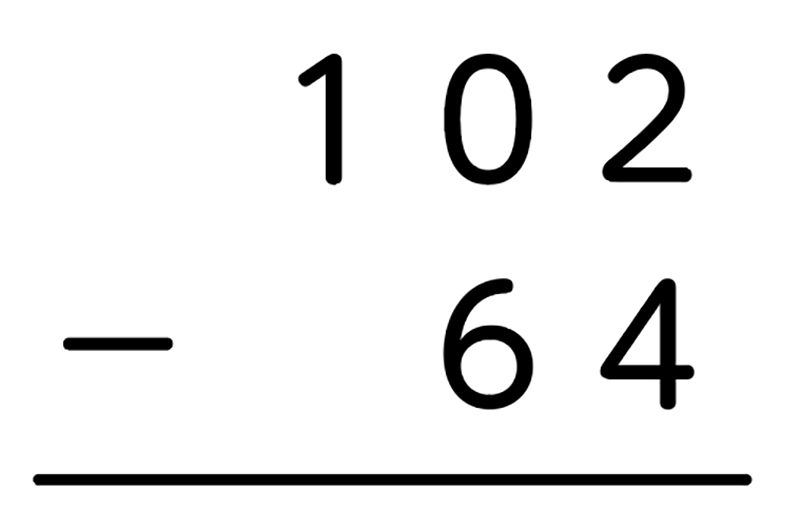
あれ。でも、2から4が引けない。
十の位から借りてくればいいと思います。
うん。だけど、十の位がないの。
えっ。本当だ。十の位が0だ。
これは大変。どうしましょう。

十の位が0のときの筆算のしかたを考えよう。
見通し
前回までは、十の位から繰り下げてこられたけれど、今回はできません。筆算では、計算できないのでしょうか。
十の位がだめなら、百の位から繰り下げたらいいと思います。
100円から64円引けばいいです。
それ、筆算でどうやるの。
なるほど。百の位はあるのだから、百の位から繰り下げればできそうですか。
できます。
自力解決の様子
A つまずいている子
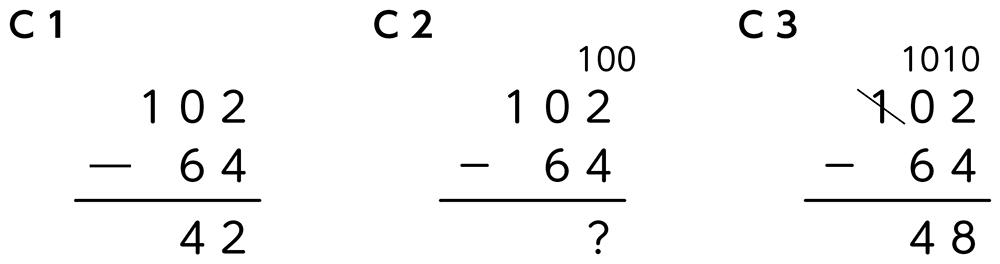
B 素朴に解いている子
正しく筆算をしている。
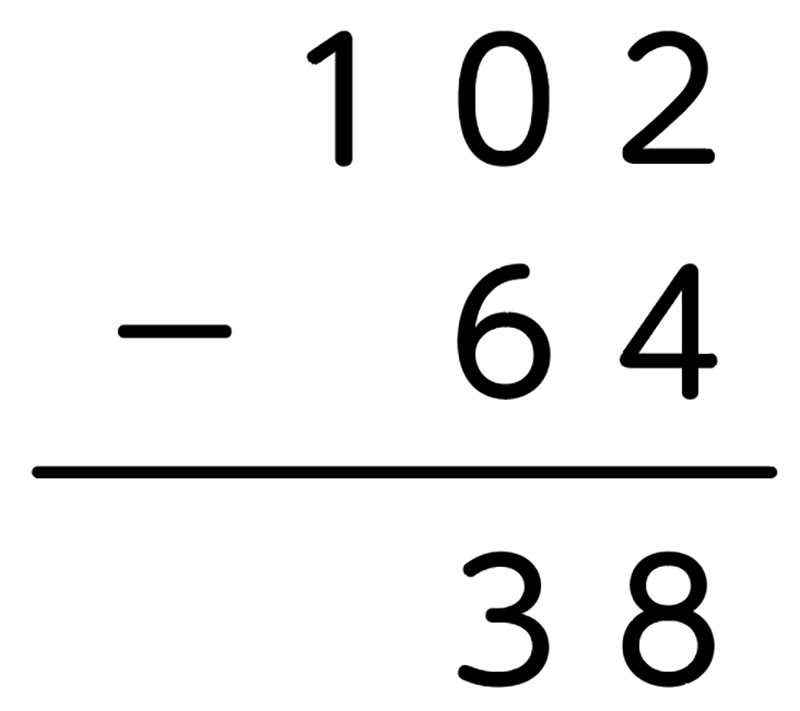
C ねらい通り解いている子
正しく筆算をし、筆算のしかたを説明することができている。
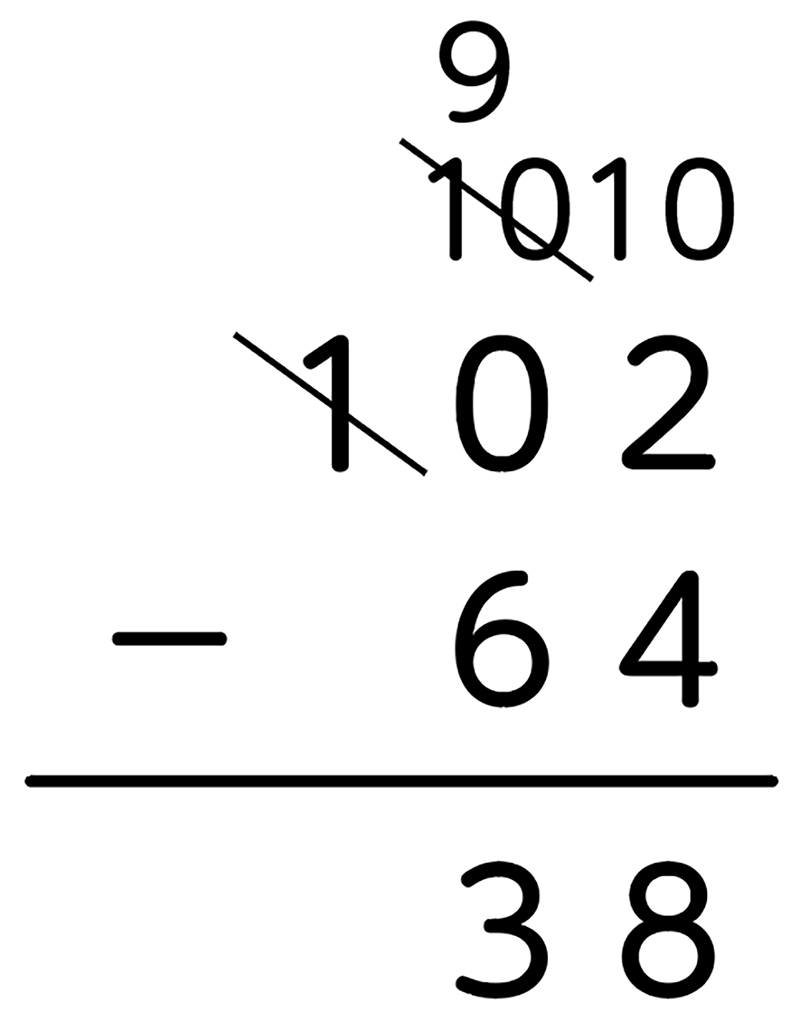
学び合いの計画
イラスト/横井智美

