小6算数「分数のわり算」指導アイデア《除数の分子が１のときの分数÷分数の計算》

執筆／新潟県新潟市立新津第一小学校教諭・古川智子
監修／文部科学省教科調査官・笠井健一、新潟県新潟市立新津第一小学校校長・間嶋哲

単元の展開

第１時　（本時）除数の分子が１のときの（分数）÷（分数）の式の意味と、計算のしかたを考える。
▼
第２時　（分数）÷（分数）の計算のしかたを考える。
▼
第３時　除数が仮分数の計算の意味を理解する。
▼
第４時　帯分数で割る計算のしかたを考える。
▼
第５時　帯分数での除法の文章題を、線分図や表を基に解く。
▼
第６時　被除数、除数、商の関係を調べる。
▼
第７時　分数の乗法や除法を適用する問題で、演算決定をし、問題解決することができる。
▼
第８時　既習事項の確かめをする。

本時のねらい

問題場面から、面積図や数直線を使って意味を考えたり、計算のしかたを面積図や数直線、わり算のきまりを使って、考えたりすることができる。

評価規準

（分数）÷（分数）の計算のしかたについて、 言葉や図で表すことができる。

本時の展開

[MATH]\(\frac{2}{5}\)[/MATH]㎡のへいをぬるのに、ペンキを□dL使います。このペンキ１dLあたり、何㎡ぬれますか。

※既習事項の復習として整数の値を入れる。

・割る数が分数になることを、既習事項（分数÷整数）を使って確認しましょう。
・どのように考えてきたかを、言葉や数字だけで説明させるだけでなく、対応数直線と結び付けながらふり返ると、より理解が深まります。
・次の２つの理由を押さえていくことが大切です。
①対応数直線を使って、１dLあたりのペンキの量を求めたいから、[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{1}{4}\)[/MATH]
②求めたい数値を□として、□×[MATH]\(\frac{1}{4}\)[/MATH]＝[MATH]\(\frac{2}{5}\)[/MATH]となるので、□＝[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{1}{4}\)[/MATH]

[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{1}{4}\)[/MATH]の対応数直線

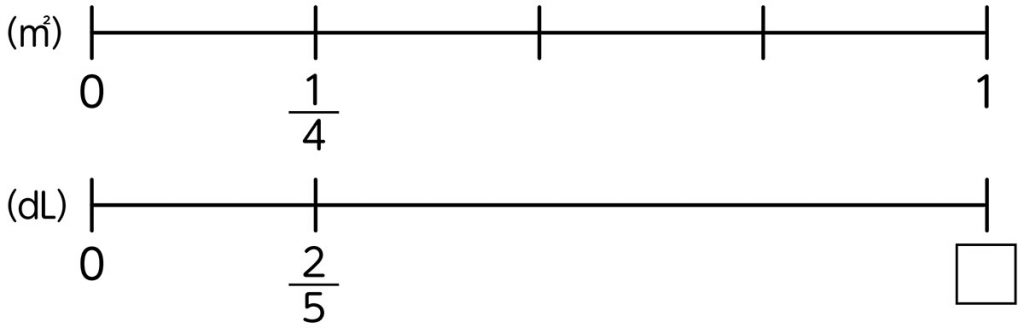
[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{1}{4}\)[/MATH]は、どうやって計算したらよいのだろうか。

見通し

見通しをもつ段階で、「わり算を既習の分数のかけ算にできる」という見方・考え方を引き出し、働かせて、解決を図りましょう。

自力解決の様子

A つまずいている子

割る数が分数になることで、混乱している。意味を理解できず、数直線や図を用いて計算することができない。

Ｂ 図を使って解いている子

面積図や数直線を使って、答えは求めることができる。しかし、どのように計算をしたらよいか説明ができない。

Ｃ ねらい通り解いている子

割る数を１にすることに着目して、[MATH]\(\frac{1}{4}\)[/MATH]に逆数をかけて、÷１の形に直して考える。わり算のきまりを使って計算することができる。

学び合いの計画

割る数が分数になったときの除法の意味を考えていく場面です。

分数で割ることの意味は難しく、子供たちは、「分数の割り算はひっくり返してかければよい」と形式的に覚えがちです。そこで、数直線や図と数を関連させながら話し合わせ、分数のわり算の理解を深めていきましょう。

(分数）÷（整数）の場面から、[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{1}{4}\)[/MATH]＝[MATH]\(\frac{2}{5}\)[/MATH]×４となりそうだということを確認します。そこで、「『÷[MATH]\(\frac{1}{4}\)[/MATH]』が『×[MATH]\(\frac{4}{1}\)[/MATH]』に変身するのだろうか」と投げかけて、「答えはいくつになるか説明できるかな」と問います。

五年生の小数の学習で、両方の辺を10倍したら整数に直せたという既習事項を想起させるなど、今回も割る数が分数でも、整数に直せば計算できそうだということを気付かせていきます。

計算のしかたについては、除法に関して成り立つ性質を活用し、「割られる数と割る数１で割って、４をかける」「割られる数と割る数に[MATH]\(\frac{4}{1}\)[/MATH]をかけて、割る数を１にする」など、「分数÷整数」「分数×整数」や「分数×分数」に変えていけば、既習したことを生かして計算できることを確認していきましょう。

ノート例

全体発表とそれぞれの考えの関連付け

• [MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{1}{4}\)[/MATH]＝（[MATH]\(\frac{2}{5}\)[/MATH]×４）÷（[MATH]\(\frac{1}{4}\)[/MATH]×４）＝[MATH]\(\frac{2}{5}\)[/MATH]×４÷１＝[MATH]\(\frac{2}{5}\)[/MATH]×４＝[MATH]\(\frac{8}{5}\)[/MATH]
• [MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{1}{4}\)[/MATH]＝（[MATH]\(\frac{2}{5}\)[/MATH]×20）÷（[MATH]\(\frac{1}{4}\)[/MATH]×20）＝８÷５＝[MATH]\(\frac{8}{5}\)[/MATH]

割る数と割られる数に４や20を掛けた根拠を問い、「今までに習った分数のかけ算やわり算が使えるから」と、子供たちに根拠を確認しましょう。
式だけの操作で考えている子供もいると思われるので、式と図を関連付けながら、それぞれ対応させながら意味を理解させていきましょう。

割る数が分数でも、わり算をすることができる。
対応数直線や図を使ったり、割る数をなん倍すれば１になるかを考えたりすると、分数のかけ算を使って計算できる。

評価問題

[MATH]\(\frac{3}{5}\)[/MATH]÷[MATH]\(\frac{1}{3}\)[/MATH]の商を求め、計算のしかたを説明しましょう。

子供に期待する解答の具体例

[MATH]\(\frac{3}{5}\)[/MATH]÷[MATH]\(\frac{1}{3}\)[/MATH]＝（[MATH]\(\frac{3}{5}\)[/MATH]×３）÷（[MATH]\(\frac{1}{3}\)[/MATH]×３）＝[MATH]\(\frac{3}{5}\)[/MATH]×３÷１＝[MATH]\(\frac{3}{5}\)[/MATH]×３＝＝[MATH]\(\frac{9}{5}\)[/MATH]

感想例

• 分数のかけ算のときと同じように、分数でもわり算をしてもよいことが分かり、数直線やわり算のきまりを使って説明したので、その意味が分かりました。
• 分数のわり算は割る数が分数でも、整数に直せば、今まで学習したことを使って計算できることが分かりました。
• アさんの考え方は、÷１になって簡単なので、すごいなと思いました。

１人１台端末活用ポイント

Googleアプリの「Jamboard(ジャムボード)」は、みんなで共同作業できるオンラインのホワイトボードです。最大20枚のフレーム（白紙のページ）を作成することができ、それぞれ同時に編集活動が可能です。話合い活動のときに、グループやクラスみんなで考えを出し合ったり、意見を整理したりすることができます。

ホワイトボードの上に、自由かつ簡単に文字や図などを書き込めることはもちろん、付箋機能もあるため、話し合ったことが視覚的にも分かりやすく表示できます。

分数のわり算では、「対応数直線」を提示し、付箋機能で当てはまる数字を対応させてみたり、「対応数直線」「面積図」のフレーム（ページ）を作って、それぞれ図にかき込みながら話合いをしたりして、考えをまとめることに活用してみてはいかがでしょうか。

グループごとにフレーム№を指定すると、グループごとの話合いもでき、全体で発表のときも、各グループのフレーム（ページ）を見れば、どのような話合いをしたかが分かりやすいです。

イラスト／横井智美

【関連記事】
【文部科学省教科調査官監修】１人１台端末時代の教科指導ヒントとアイデアシリーズはこちら！
・小4外国語活動 Unit 7「What do you want?」指導アイデア
・小5外国語 Unit 7「Welcome to Japan.」指導アイデア②
・小5外国語 Unit 7「Welcome to Japan.」指導アイデア①
・小6 国語科「狂言　柿山伏」「柿山伏について」板書例＆全時間の指導アイデア
・小3外国語活動 Unit 7「This is for you.」指導アイデア
・小4体育「ゲーム（ゴール型ゲーム）」指導アイデア①
・小4体育「ゲーム（ゴール型ゲーム）」指導アイデア②
・小2体育「器械・器具を使っての運動遊び（跳び箱を使った運動遊び）」指導アイデア①
・小2体育「器械・器具を使っての運動遊び（跳び箱を使った運動遊び）」指導アイデア②
・小1体育「器械・器具を使っての運動遊び（マットを使った運動遊び）」指導アイデア①
>>もっと見る