小5算数「合同な図形」指導アイデア
執筆/新潟県公立小学校教諭・二瓶亮
編集委員/文部科学省教科調査官・笠井健一、新潟県公立小学校校長・間嶋哲
目次
本時のねらいと評価規準
(本時の位置 3/7時)
ねらい
合同な三角形をかくためには、すべての構成要素を用いる必要がないことを理解し、合同な図形をかく。
評価規準
合同な三角形をかくためには、1つの辺の長さと、あと2つの構成要素を用いればかくことができることを理解し、合同な三角形を作図する。
問題
三角形ABCと合同な三角形を作図しましょう。
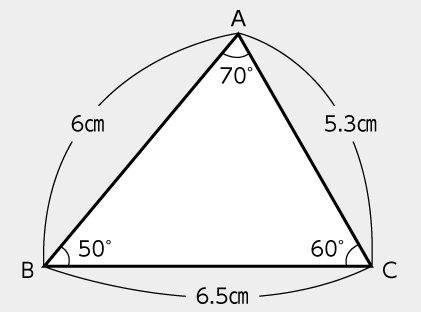
第3学年では主に差異点や共通点を基に、問題を見いだすことができるようにするため、複数の事物・現象を比較し、その差異点や共通点を捉えることが大切です。辺の長さや角度など、数値は一切示さずに提示しましょう。作図に必要な要素について、子供から引き出していく中で作図のイメージを膨らませていくことが大切です。
どんな情報がほしいですか。
辺の長さと角度が知りたい。
では、辺BCの長さだけ教えます。
まだ足りないよ。それだと頂点Aの位置が決まらない。
頂点Aの位置を決めるには、あといくつの情報が必要ですか?
あと3つか4つあればかけると思う。
あと2つ知りたい。
本時の学習のねらい
合同な三角形を作図するには、辺BCの他に、あといくつの条件が必要だろうか。
見通し
2つや3つ、4つと言っている人がいますね。どうしてあと1つではできないのですか?
それだと頂点Aの位置がはっきりと決まらない。たとえば、辺ABの長さが分かったとしても、どんな角度(角B)で辺ABを引けばいいのか分からない。
もし角度を教えてもらっても、辺の長さが分からないと、どこまで引くのかが分からない。
そうそう。だから、辺の長さと角度を1つずつ教えてほしいな。
別のかき方もできそうだよね。コンパスを使えば……。辺の長さをあと2つ知りたいな。
三角形ABCの図を渡します。自分で必要だと思う条件を選んで作図しましょう。合同な図形を作図する際に、どの辺の長さや角の大きさを使ったのかをノートに残しておきましょう。
自力解決の様子
A つまずいている子
2つの辺の長さと、2つの底角の大きさなど、3つを超える条件を使ってかく。
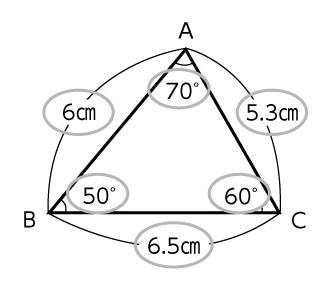
B 素朴に解いている子
合同条件ではない3つの条件を使ってかく。
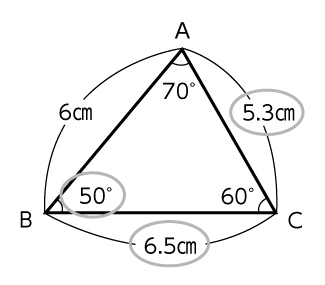
C ねらい通り解いている子
3辺の長さ、2辺とその間の角、1辺とその両端の角、といった合同条件を使ってかく。
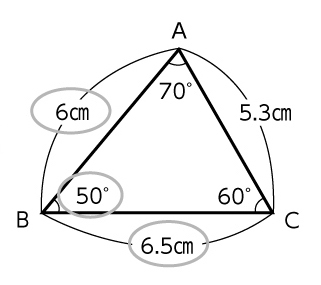
学び合いの計画
イラスト/横井智美
『教育技術 小五小六』 2021年6/7月号より






