小6算数「円の面積」指導アイデア《円を分割・変形して面積を求める》
執筆/新潟県佐渡市立金井小学校教諭・名古屋祥吾
監修/文部科学省教科調査官・笠井健一、新潟県新潟市立新津第一小学校校長・間嶋哲

目次
単元の展開
第1時 方眼を用いて、半径5㎝の円の面積を求める。
▼
第2時(本時)半径10㎝の円を16等分した扇形を敷き詰め、既習の図形に変形させ、面積を求める。
▼
第3時 前時に等積変形させ、面積を求めたそれぞれの式から、求積公式を導き出す。
▼
第4時 正方形と四分円を組み合わせた形の面積を求める。
▼
第5時 形の概形を基本的な図形と捉えて、面積を概測する方法を理解する。
▼
第6時 円の求積公式を用いて、複合図形の面積を求める。
本時のねらい
半径10㎝の円を既習の図形に並べ替えたそれぞれの場合について、図形を求めるために必要な「底辺」や「高さ」、「縦」や「横」の長さが円のどの部分を表しているかを話し合う活動を通し、並び替えたそれぞれの図形から円の面積を求めることができる。
評価規準
半径2㎝の円を縦に長い平行四辺形に変形させた場合(下図)について、「底辺」と「高さ」が円のどこの部分を表しているかを式に表し、面積を求めることができる。
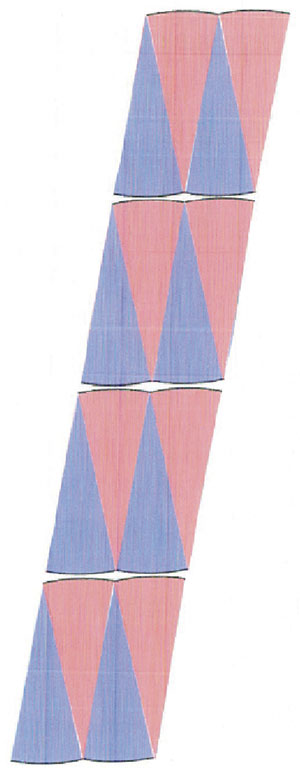

半径10㎝の円の面積を、方眼を使わないで求めよう。

「底辺」や「高さ」、「縦」や「横」の長さはいくつになるのだろう。
見通し
半径10㎝の円の方眼を使わないで、面積を求める方法はありませんか。
平行四辺形の面積を求めたとき、切って長方形に変形させて考えました。
そうでしたね。円も長方形などの知っている形に変形させられますか。
変形できそうです。
ここに16等分したものがあるので、これを敷き詰めて別の形に変形させてみましょう。例えば、このように敷き詰めていくと、どんな図形になりそうですか。

平行四辺形になりそうです。
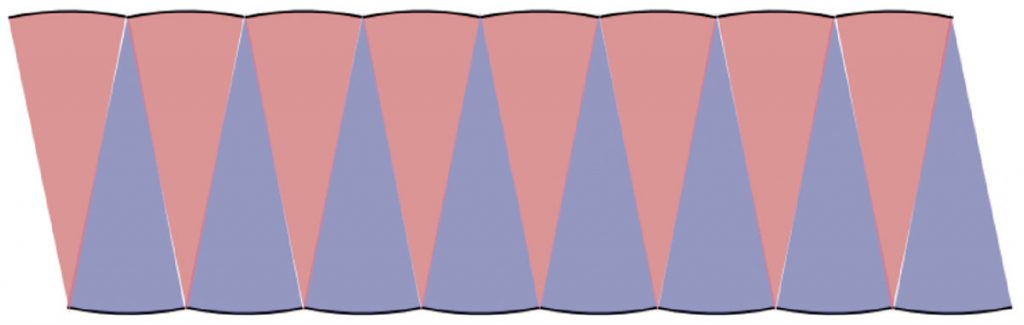
これって、平行四辺形って言っていいのかな。辺が波波になっているよ。
そうですね。皆さんに渡した円は16等分したものでしたが、円を32等分、64等分と細かくしていくと、波波の部分はどうなるか、確認してみましょう。
1人1台端末活用ポイント1
「JAVA実験室 円の面積」を活用する。https://javalab.org/ja/area_of_circle_ja/
底辺が波波に見える。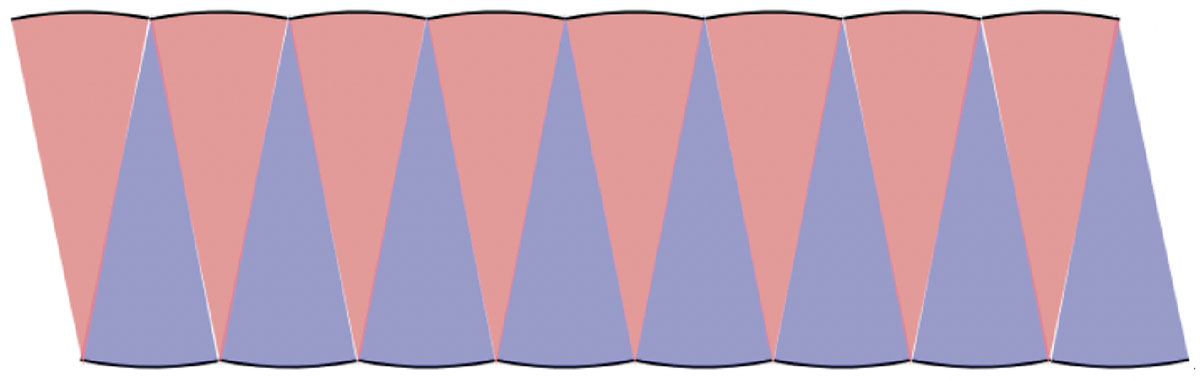
底辺が直線のように見える。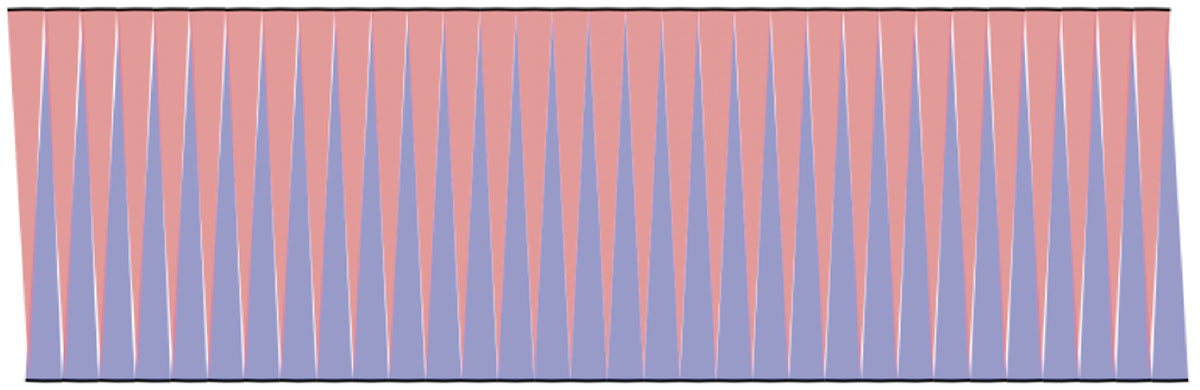
最も大きく分けて4等分、最も細かく分けて128等分することができます。細かくすればするほど、直線に近くなってくることが実感できます。
細かくしていくと、波波の部分は直線に見えてきて、平行四辺形に見えるね。
では、平行四辺形のほかに、どんな図形ができそうですか。
三角形ができました。
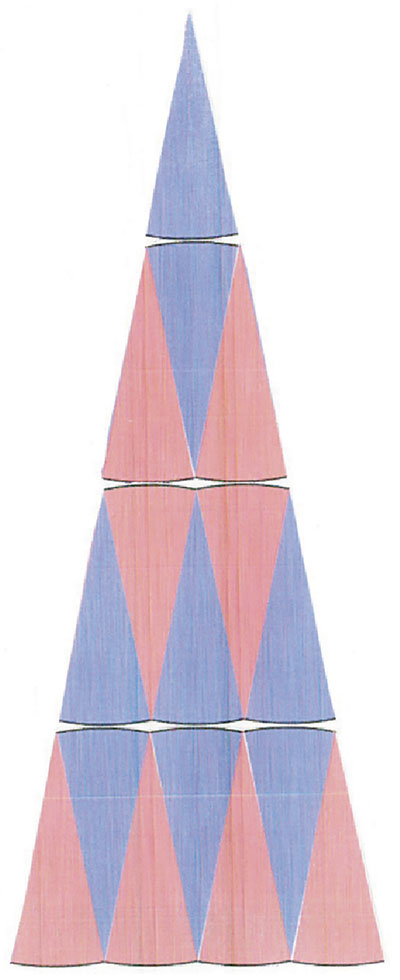
台形ができました。

さまざまな形に変形できましたね。平行四辺形に変形させた人は、どのような公式で面積を求めるとよいですか。
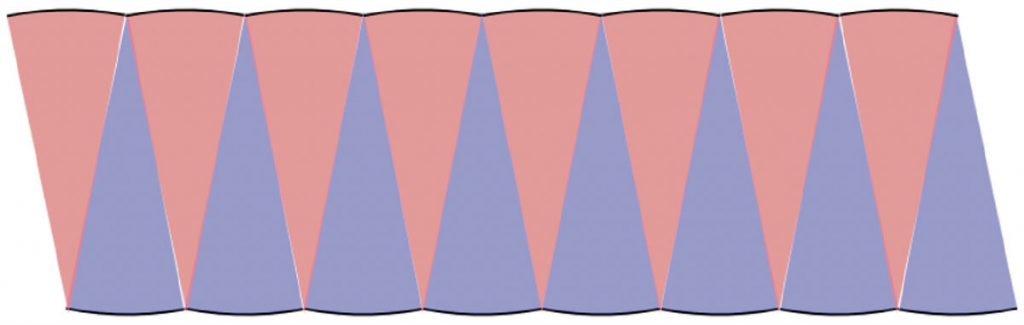
底辺×高さです。
この平行四辺形に並び替えた図形では、底辺と高さはどの部分になりますか。
この部分です。
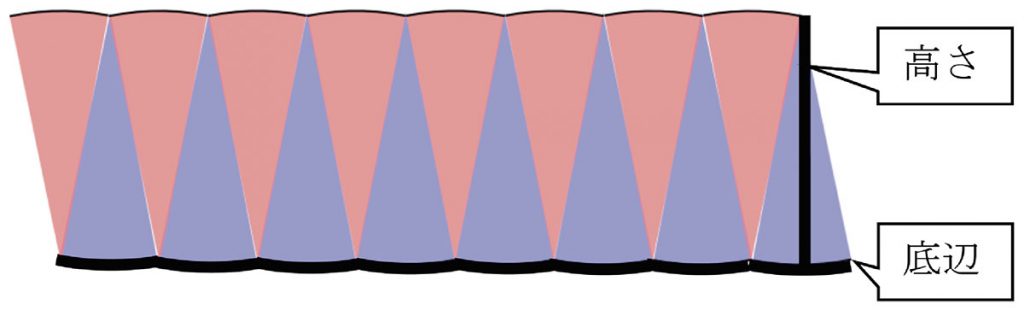
ほかの図形は、どのような公式で求めるとよいですか。また、それは、並び替えた図形のどの部分ですか。自分が並び替えた図形の面積を求めましょう。
自力解決の様子(平行四辺形に変形させた子供の場合)
A つまずいている子
- 高さが半径と等しいことに気付けない。
- 底辺の長さを求める見当が付かない。
B 素朴に解いている子
高さに当たる部分が、半径の長さと等しいことが分かる。また、底辺の長さを求める際、扇形1つ分の弧の長さを求めてから、底辺全体の長さを求めている。
底辺の長さは、20×3.14÷16=3.925 3.925×8=31.4です。高さは、10㎝です。平行四辺形の面積は、底辺×高さで求められるので、31.4×10=314
C ねらい通り解いている子
高さに当たる部分が、半径の長さと等しいことが分かる。また、底辺の長さは円周の半分と等しい長さであることに気付き、長さを求めている。
底辺の長さは、20×3.14÷2=31.4です。高さは、10㎝です。平行四辺形の面積は、底辺×高さで求められるので、3.14×10=314
学び合いの計画
イラスト/横井智美

