小5算数「小数のかけ算」指導アイデア《整数×小数の計算のしかた》

執筆／福岡教育大学附属福岡小学校教諭・西島大祐
監修／文部科学省教科調査官・笠井健一
　福岡教育大学教授・清水紀宏

単元の展開

第１時　小数をかけることの意味を図や式を用いて考え、説明する。
▼
第２時（本時）整数×小数の計算のしかたを、数直線を用いて考える。
▼
第３、４時　小数×小数の筆算のしかたを、乗法の性質を基に考える。
▼
第５時　末尾の0を処理したり、0を補ったりする場合の筆算のしかたを話し合う。
▼
第６時　純小数をかけると、積は被乗数より小さくなることを理解し、説明する。
▼
第７時　長方形や直方体の辺の長さが小数の場合も、面積や体積の公式を適用できることを理解し、説明する。
▼
第８時　整数について成り立つ計算の法則は、小数の場合でも成り立つか話し合う。

本時のねらい

乗法の意味に着目し、整数×小数の計算のしかたを、既習の計算や数直線を用いて考え、説明することができる。

評価規準

整数×小数の計算のしかたを、小数の構成（0.1のいくつ分）や乗法の性質（乗数を10倍すると積も10倍）に着目して、整数の計算に帰着して考え、説明している。（思考・判断・表現）

１mのねだんが80円のリボンを2.3m買ったときの代金は、なん円になるでしょう。

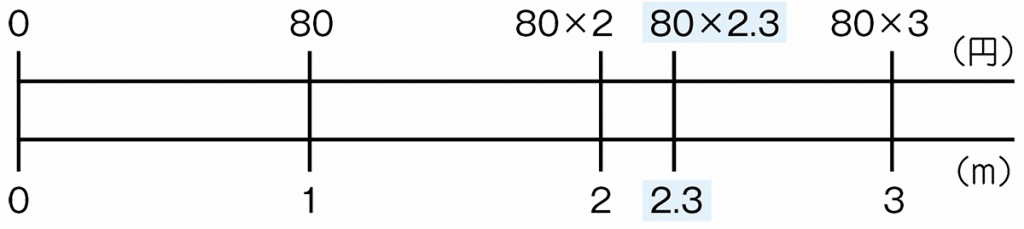
※前回の授業では、小数をかけることの意味を捉えることをねらいとしています。そのことについて数直線を用いながらふり返ることで、本時学習の見通しをもつことができるようにします。

見通し

※見通しの段階では、数直線が使えるのではないかという方法の見通しや、既習の整数の計算を基に、およそ200円になるのではないかという結果の見通しももたせておくとよいでしょう。

整数×小数の計算のしかたについて、数直線を使って説明しよう。

自力解決の様子

A つまずいている子

どのように考えるとよいか分からず、計算の答えを求めることができていない。

Ｂ 素朴に解いている子

数直線や式を使って答えを求めることはできているが、その理由を説明することはできてない。

Ｃ ねらい通り解いている子

0.1mの代金を基に、その23倍をしたり、乗法の性質を使ったりして、多様な方法で考えることができている。

学び合いの計画

本時では2.3mを0.1mの23個分と考えたり、23mの10分の１と考えたりして、既習である整数をかける計算のしかたを基にして考えることが重要です。そのため、学び合いにおいては、ノートを見せ合ったり、数直線を指差したりしながら、なぜその計算方法になるのかを説明し合うことが大切です。

イラスト／横井智美